Giúp em với ạ em đang cần gấp . Làm hết giúp em nha 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BT
5
Những câu hỏi liên quan
BT
7
13 tháng 7 2021
1) Ta có: \(\sqrt{2x+5}=\sqrt{3-x}\)
\(\Leftrightarrow2x+5=3-x\)
\(\Leftrightarrow2x+x=3-5\)
\(\Leftrightarrow3x=-2\)
hay \(x=-\dfrac{2}{3}\)
2) Ta có: \(\sqrt{2x-5}=\sqrt{x-1}\)
\(\Leftrightarrow2x-5=x-1\)
\(\Leftrightarrow2x-x=-1+5\)
\(\Leftrightarrow x=4\)
PN
23 tháng 8 2021
3 , \(PT\left(đk:\frac{16}{3}\ge x\ge3\right)< =>x^2-3x=16-3x\)
\(< =>x^2-16=0< =>\left(x-4\right)\left(x+4\right)=0< =>\orbr{\begin{cases}x=4\left(tm\right)\\x=-4\left(ktm\right)\end{cases}}\)
4 , \(PT\left(đk:...\right)< =>2x^2-3=4x-3< =>2x^2-4x=0\)
\(< =>2x\left(x-2\right)=0< =>\orbr{\begin{cases}x=0\left(...\right)\\x=2\left(...\right)\end{cases}}\)
bạn tự tìm đk rồi đối chiếu nhé :P
KM
0
TG
0
D
2
NA
10 tháng 3 2022
bài 3:
tổng số giờ đã chảy đc từ 2 vòi : 1+1=2(giờ)
tổng số phần bể đã chảy được từ 2 vòi : \(\dfrac{1}{5}+\dfrac{1}{7}=\dfrac{7}{35}+\dfrac{5}{35}=\dfrac{12}{35}\left(ph\text{ần} b\text{ể}\right)\)
nếu chảy cùng lúc mỗi giờ chảy được : \(\dfrac{12}{35}:2=\dfrac{12}{35\cdot2}=\dfrac{6}{35}\left(ph\text{ần}b\text{ể}\right)\)
bài 4:
cách 1:
độ dài đoạn AB là : \(\dfrac{3}{4}+\dfrac{9}{8}=\dfrac{18}{24}+\dfrac{27}{24}=\dfrac{45}{24}\left(m\right)\)
diện tích ABCD là : \(\dfrac{45}{27}\cdot\dfrac{4}{7}=\dfrac{15}{14}\left(m^2\right)\)
cách 2:
diện tích AEFD là : \(\dfrac{3}{4}\cdot\dfrac{4}{7}=\dfrac{3}{7}\left(m^2\right)\)
diện tích EBCF là : \(\dfrac{9}{8}\cdot\dfrac{4}{7}=\dfrac{9}{14}\left(m^2\right)\)
diện tích ABCD là : \(\dfrac{3}{7}+\dfrac{9}{14}=\dfrac{15}{14}\left(m^2\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2021
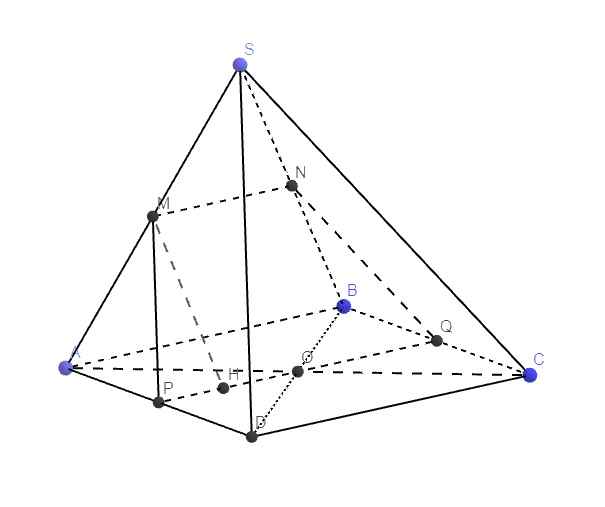
MN là đường trung bình tam giác SAB \(\Rightarrow\) MN song song và bằng 1 nửa AB
Gọi P là trung điểm AD \(\Rightarrow PQ||AB\Rightarrow PQ||MN\Rightarrow P\in\left(MNQ\right)\)
\(\Rightarrow\) MNQP là thiết diện của chóp và (MNQ)
Do MN song song PQ \(\Rightarrow\) MNQP là hình thang
Lại có M, P là trung điểm SA, AD \(\Rightarrow MP=\dfrac{1}{2}SD\)
Tương tự \(NQ=\dfrac{1}{2}SC\Rightarrow MP=NQ=\dfrac{b\sqrt{3}}{2}\)
\(\Rightarrow\) Thiết diện là hình thang cân
\(PQ=AB=a\) ; \(MN=\dfrac{1}{2}PQ=\dfrac{a}{2}\)
Kẻ \(MH\perp PQ\Rightarrow PH=\dfrac{PQ-MN}{2}=\dfrac{a}{4}\)
\(\Rightarrow MH=\sqrt{MP^2-PH^2}=\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)
\(S=\dfrac{1}{2}\left(MN+PQ\right).MH=\dfrac{3a}{4}.\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)
1) Ta có: \(\sqrt{4x}=\sqrt{5}\)
nên 4x=5
hay \(x=\dfrac{5}{4}\)
2) Ta có: \(\sqrt{16x}=8\)
nên 16x=64
hay x=4
3, \(2\sqrt{x}=\sqrt{9x}-3\left(đk:x\ge0\right)\)
\(< =>2\sqrt{x}-3\sqrt{x}+3=0\)
\(< =>3-\sqrt{x}=0< =>x=9\)(tmđk)
4, \(\sqrt{3x-1}=4\left(đk:x\ge\frac{1}{3}\right)\)
\(< =>3x-1=16< =>3x-17=0\)
\(< =>x=\frac{17}{3}\)(tmđk)