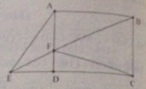
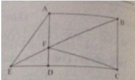
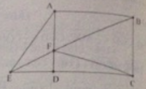
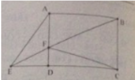
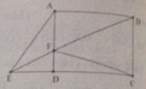
Cho hình chữ nhật ABCD . Biết F là một điểm bất kì trên cạnh AB , BF và cắt tại CD kéo dài tại điẻmE . Nối điểm A với điểm E .Tính diện tích của hình tam giác AEF , biết rằng AF = 3cm , BC=5cm , AB= 7cm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 5 2018
Ta có: S(ABE) = S(ABC) = ½ AB BC = 17,5 (cm²)
S(ABF) = ½ AB AF = 10,5 (cm²)
Suy ra diện tích tam giác AEF là
S(AEF) = S(ABE) – S(ABF) = 17,5 – 10,5 = 7 (cm²)
Đáp số: 7 cm².
B
21 tháng 8 2017
Giải Ta có:
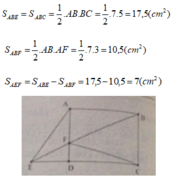
S(ABE) = S(ABC) = ½ AB
BC = 17,5 (cm²) S(ABF) = ½ AB AF = 10,5 (cm²)
Suy ra diện tích tam giác AEF là
S(AEF) = S(ABE) – S(ABF) = 17,5 – 10,5 = 7 (cm²)
Đáp số: 7 cm².
1 tháng 6 2019
Tam giác EAB cạnh đáy BA chiều cao nằm ngoài tam giác và cũng chính bằng chiều rộng BC của hình chữ nhật = 5cm.
Diện tích hình tam giác EBA là: 7 x 5 : 2 = 17,5 cm2
Diẹn tích hình tam giác FAB là: 3 x 7:2 = 10,5cm2
Diễn tích hình tam giác AEF: 17,5 - 10,5 = 7cm2
Đáp số: 7cm2
~ học tốt~
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
17 tháng 5 2022
Vì đề bài không rõ ràng AD là chiều dài hay chiều rộng nên trong bài này tôi coi AD là chiều rông.
\(S_{ABCD}=ADxAB=5x7=35cm^2\)
Ta có \(S_{ABC}=\dfrac{1}{2}xS_{ABCD}\)
Hai tg ABC và tg FBC có chung BC, đường cao từ A->BC = đường cao từ F->BC nên
\(S_{FBC}=S_{ABC}=\dfrac{1}{2}xS_{ABCD}\)
Hai tg ABF và tg FBC có đường cao từ B->AD = đường cao từ F->BC nên
\(\dfrac{S_{ABF}}{S_{FBC}}=\dfrac{AF}{BC}=\dfrac{3}{5}\Rightarrow S_{ABF}=\dfrac{3}{5}xS_{FBC}=\dfrac{3}{5}x\dfrac{1}{2}xS_{ABCD}=\dfrac{3}{10}xS_{ABCD}\)
Hai tg này có chung BF nên
\(\dfrac{S_{ABF}}{S_{FBC}}=\) đường cao từ A->BE / đường cao từ C->BE \(=\dfrac{3}{5}\)
=> đường cao từ A->BE = \(\dfrac{3}{5}\) đường cao từ C->BE
Hai tg AEF và tg DEF có chung đường cao từ E->AB nên
\(\dfrac{S_{AEF}}{S_{DEF}}=\dfrac{AF}{DF}=\dfrac{3}{2}\)
Hai tg này có chung EF nên
\(\dfrac{S_{AEF}}{S_{DEF}}=\) đường cao từ A->BE / đường cao từ D->BE\(=\dfrac{3}{2}\)
=> đường cao từ D->BE = \(\dfrac{2}{3}\) đường cao từ A-> BE = \(\dfrac{2}{3}x\dfrac{3}{5}\) đường cao từ C->BE \(=\dfrac{2}{5}\) đường cao từ C->BE
Hai tg DEF và tg CEF có chung EF nên
\(\dfrac{S_{DEF}}{S_{FCE}}=\)đường cao từ D->BE / đường cao từ C->BE \(=\dfrac{2}{5}\)
Chia diện tích tg DEF thành 2 phần thì diện tích tg CEF là 5 phần
=> Số phần chỉ diện tích tg CDF là
5-2=3 phần
\(\Rightarrow\dfrac{S_{DEF}}{S_{CDF}}=\dfrac{2}{3}\)
Hai tg này có chung DF nên
\(\dfrac{S_{DEF}}{S_{CDF}}=\) đường cao từ E->AD / đường cao từ C->AD \(=\dfrac{2}{3}\)
Mà đường cao từ C->AD = đường cao từ B->AD
=> đường cao từ E->AD / đường cao từ B->AD = \(\dfrac{2}{3}\)
Hai tg AEF và tg ABF có chung AF nên
\(\dfrac{S_{AEF}}{S_{ABF}}=\)đường cao từ E->AD / đường cao từ B->AD \(=\dfrac{2}{3}\)
\(\Rightarrow S_{AEF}=\dfrac{2}{3}xS_{ABF}=\dfrac{2}{3}x\dfrac{3}{10}xS_{ABCD}=\dfrac{1}{5}xS_{ABCD}=\dfrac{1}{5}x35=7cm^2\)
Hai tg AEF và tg EFC có chung EF nên
\(\dfrac{S_{AEF}}{S_{EFC}}=\)đường cao từ A->BE / đường cao từ C->BE \(=\dfrac{3}{5}\)
\(\Rightarrow S_{EFC}=\dfrac{5}{3}xS_{AEF}=\dfrac{5}{3}x7=\dfrac{35}{3}cm^2\)
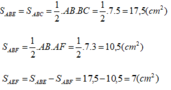
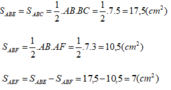
BF cắt CD tại điểm E ?
AB và CD song song nhau,nếu lấy F trên AB thì không thể cho BF cắt CD được :