Cho ∆ABC cân tại A. Gọi H là hình chiếu của B trên AC. Tính cạnh đáy BC của tam giác biết AH = 7cm, HC = 2cm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nguyễn Quỳnh Nga làm đc ko mà Spam?
Giải:
Do ABCABC cân nên AB=AC=7+2=9 cm
H là hình chiếu của B lên AC nên BH vuông góc AC
Áp dụng Py - ta - go, ta có:
\(BC=\sqrt{BH^2+2^2}=6\)

hình ạn tư vẽ nha
vì ABC cân nên AB = AC = AH + HC = 9 cm
Xét tam giác ABH : có góc AHB = 90 độ ( vì H là hình chiếu của B trên AC)
Theo định lí Pi-ta-go ta có \(BH^2+AH^2=AB^2\)
\(\Leftrightarrow BH^2=AB^2-AH^2\)
\(\Leftrightarrow BH^2=9^2-7^2\)
\(\Leftrightarrow BH^2=32\Leftrightarrow BH=4\sqrt{2}\)
Xết tam giác BHC vuông tại H theo Định Lí Pi-ta-go ta có
\(BH^2+HC^2=BC^2\)\(\Leftrightarrow\left(4\sqrt{2}\right)^2+2^2=BC^2\)
\(\Leftrightarrow36=BC^2\)\(\Leftrightarrow BC=6cm\)

vì tam giác ABC cân tại A ==> AB=AC=7+2=9
DÙNG py-ra-go tính được BH=\(4\sqrt{2}\)
Rùi lại py-ta-go TÍNH ĐƯỢC BC=6cm

ABC cân tại A => AB = AC = AH + HC = 7 + 2 = 9
HAB vuông tại H có: \(HB^2=AB^2-AH^2=9^2-7^2=32\)
HBC vuông tại H có \(BC^2=HC^2+BH^2=2^2+32=36\)
Vậy cạnh đáy BC = \(\sqrt{36}=6\).
Ủa sao dễ nhỉ
áp dụng d/l py-ta-go trong tam giac vuongo AHC
=> BC2=AH2+HC2=72+22=53=> BC = Căn 53

Tính cạnh đáy BC của tam giác cân ABC trên các hình dưới đây. Trên hình bên trái: AH = 7cm; HC = 2cm
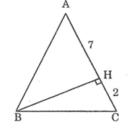
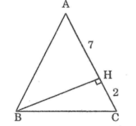

Tam giác ABC cân tại A ta có: AB = AC = CH + HA = 2 + 7 =9
Trong tam giác vuông BHA, ta có ∠(BHA) =90°
Áp dụng định lí pitago, ta có: AB2=BH2+HA2
Suy ra: BH2=AB2-AH2=92-72=81-49=32
Trong tam giác vuông BHC, ta có ∠(BHC) =90°
Áp dụng định lí pitago ta có: BC2=BH2+HC2 mà BH2 = 32, HC2 = 22 = 4
BC2 =32 + 4 =36 ⇒ BC = √36 = 6 cm

a, Áp dụng định lí Pitago vào tam giác AHC vuông tại H, ta có:
AH^2 +HC^2 =AC^2
Thay số thì tính được AH=3 cm
b, HK.AC =AH.HC (= 2 lần diện tích tam giác AHC)
Suy ra: HK .5 = 3.4
HK =2,4 cm
Xét tam giác AHK vuông tại K thì AK^2 +KH^2 =AH^2
Thay KH =2,4 cm và AH =3 cm thì được AK =1,8 cm
BH+ HC =BC nên BH+ 4 =7
BH =3 cm
Xét tam giác AHB vuông tại H tiếp tục ra: AB =căn 18 (cm)
Vậy chu vi tứ giác AHBK là:
AK +KH +HB +AB = 1,8+ 2,4+ 3+ căn 18
= 7,2 +căn 18(cm)
Mình giải vắn tắt vì ko nhiều thời gian.Mong bạn hiểu được bài.
Chúc bạn học tốt.
Ta có: AB=AC(ΔABC cân tại A)
nên AB=AH+HC=7+2=9(cm)
Xét ΔAHB vuông tại H có
\(HB^2+HA^2=AB^2\)
\(\Leftrightarrow BH^2=9^2-7^2=81-49=32\)
hay \(HB=4\sqrt{2}\left(cm\right)\)
Xét ΔBHC vuông tại H có
\(BC^2=BH^2+CH^2\)
\(\Leftrightarrow BC^2=\left(4\sqrt{2}\right)^2+2^2=36\)
hay BC=6(cm)