Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
bn vào Link này xem thử nhé :
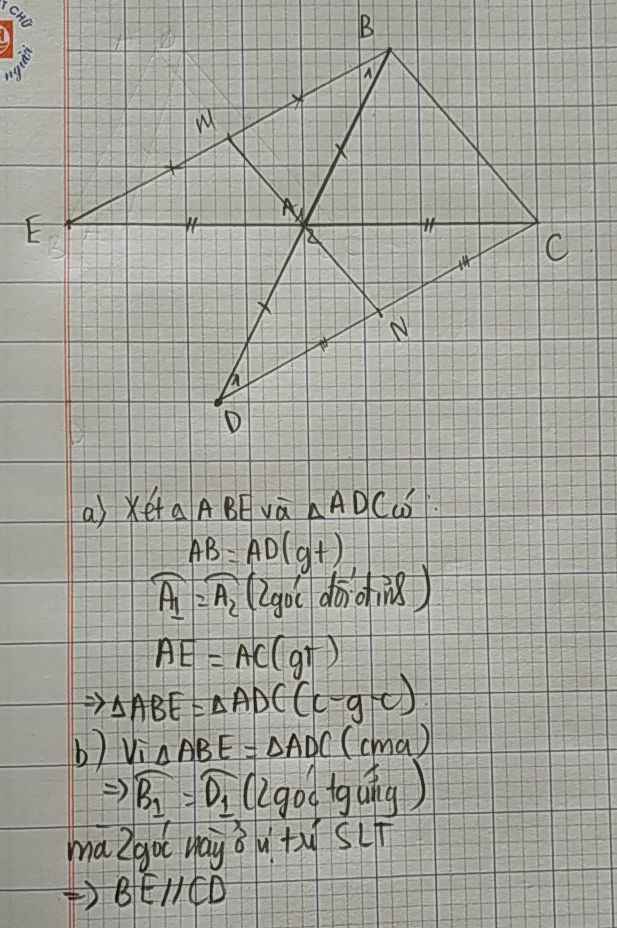
Cho tam giác đều ABC. Trên tia đối tia AB lấy điểm D và trên tia đối tia AC lấy điểm E sao cho AD = AE. Gọi M,N,P,Q lần lượt là trung điểm của các đoạn thẳng BE,AD,AC,ABa) Chứng minh rằng tứ giác BCDE là hình thang cânb) Chứng minh rằng tứ giác CNEQ là hình thangc) Tam giác MNP là tam giác đề - Tìm với Google
Hok tốt
# EllyNguyen #
Bạn kham khảo nha:
Cho tam giác đều ABC. Trên tia đối tia AB lấy điểm D và ... - Online Math
\(AD=AC\Rightarrow\)△CAD cân tại A mà AM là trung tuyến.
\(\Rightarrow\)AM cũng là đường phân giác.
\(\Rightarrow\widehat{MAE}=\dfrac{\widehat{BAE}}{2}\left(1\right)\)
\(AE=AB\Rightarrow\)△BAE cân tại A mà AN là trung tuyến.
\(\Rightarrow\)AN cũng là đường phân giác.
\(\Rightarrow\widehat{CAN}=\dfrac{\widehat{CAD}}{2}\left(2\right)\)
Ta có: \(\widehat{BAE}=\widehat{CAD}\) (đối đỉnh), nên từ (1) và (2) suy ra:
\(\widehat{EAM}=\widehat{CAN}\)
Mà \(\widehat{EAM}+\widehat{CAM}=180^0\) (kề bù)
\(\Rightarrow\widehat{CAN}+\widehat{CAM}=180^0\)
\(\Rightarrow\widehat{MAN}=180^0\)
\(\Rightarrow\)M,A,N thẳng hàng.
Câu hỏi của Phan thanh hằng - Toán lớp 8 - Học toán với OnlineMath
cm tam giác AEM= tam giác ACN => góc EAM=gocsCAN (2 góc tương ứng )
rồi ta có góc DAE+DAN+CAN=180độ (do E,A,C thẳng hàng)
lại có gócEAM=goscCAN=>DAE+DAN+EAM=180độ =>góc MAN là góc bẹt=> M,A,N thẳng hàng
bạn tham khảo link mà mk đưa cho nhé
hoiap247.com/cau-hoi/82020
nhớ k cho mk nhé
Hình bạn tự vẽ nha :)
Xét \(\Delta ABE\) có : AE = AB => \(\Delta ABE\) cân tại A
=> \(\widehat{ABE}\) = \(\widehat{AEB}\)
\(\widehat{BAC}\) = \(\widehat{ABE}\) + \(\widehat{AEB}\) = \(2\widehat{ABE}\)
Xét \(\Delta ADC\) có AD = AC => \(\Delta ADC\) cân tại A
=> \(\Delta ADC\) = \(\Delta ACD\)
\(\widehat{BAC}\) = \(\widehat{ADC}\) + \(\widehat{ACD}\) = \(2\widehat{ADC}\)
Suy ra : \(\widehat{ABE}\) = \(\widehat{ADC}\) hay \(\widehat{DBE}\) = \(\widehat{BDC}\)
=> BE // CD
\(\Delta ABE\) cân tại A có M là trung điểm của BC nên AM \(\perp\)BE
\(\Delta ADC\) cân tại A có N là trung điểm của CD nên AN \(\perp\)CD
Do đó 3 điểm M , A , N thẳng hàng
