Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Ta có\(\widehat{ADB}=\widehat{AFB}=90độ\left(gt\right)\)
Nên tứ giác ABDF nội tiếp ( 2 đỉnh EF cùng nhìn AB với 2 góc bằng nhau)
b) Ta có \(\widehat{AEDC}=90độ\)(góc nội tiếp chắn nửa đường tròn)
Nên ΔACE vuông tại C
Xét 2 tam giác vuông ABD và ACE có
\(\widehat{ABD}=\widehat{AEC}\)(cùng chắn \(\widebat{AC}\))
Nên ΔABD ~ ΔACE
Do đó \(\frac{AB}{AC}=\frac{AD}{AE}\)
Hay AB.AE=AD.AC
c) (Mình nghĩ câu này bạn ghi nhầm, theo mình thì ở đây ta phải chứng minh DF vuông góc AC)
Ta có \(\widehat{DFE}=\widehat{ABD}\)(tứ giác ABDF nội tiếp)
Mà \(\widehat{ABD}=\widehat{AEC}\)(cùng chắn \(\widebat{AC}\))
Do đó \(\widehat{DFE}=\widehat{AEC}\)
Ta lại có 2 góc này ở vị trí so le trong
Nên DF song song EC
Mà EC vuông góc AC
Suy ra DF vuông góc AC
Chọn đáp án D
* Chứng minh các tứ giác ABHF và BMFO nội tiếp.
- Từ giả thiết suy ra: 
=> H và F thuộc đường tròn đường kính AB (quỹ tích cung chứa góc)
Vậy tứ giác ABHF nội tiếp đường tròn đường kính AB
- Gọi M là trung điểm của BC (gt), suy ra: OM ⊥ BC
Khi đó: 
Nên M, F thuộc đường tròn đường kính OB(quỹ tích cung chứa góc).
Vậy tứ giác BMOF nội tiếp đường tròn đường kính OB
* Chứng minh HE // BD.
Dễ chứng minh tứ giác ACEH nội tiếp đường tròn đường kính AC.
Và chúng ở vị trí so le trong suy ra: HE // BD
a)
Xét (O) có
M là trung điểm của dây BC(gt)
nên OM\(\perp\)BC(Định lí đường kính vuông góc với dây)
Xét tứ giác BMOF có
\(\widehat{BFO}+\widehat{BMO}=180^0\left(90^0+90^0=180^0\right)\)
nên BMOF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Cho tam giác ABC có 3 góc nhọn (AB<AC) nội tiếp đường tròn tâm O. Kẻ đường cao AH của tam giác và đường kính AD của đường tròn (O). Gọi E,F lần lượt là chân đường vuông góc kẻ từ C và B xuống đường thẳng AD. Gọi M là trung điểm ÁD
a) Chứng minh tứ giác BMFO nội tiếp
b) chứng minh HE//BD
c) Chứng minh $S=\frac{AB.AC.BC}{4R}$S=AB.AC.BC4R ( Với S là diện tích tam giác ABC, R là bán kính đường tròn (O) )
Chịu @ _@
Bạn nào lướt qua thì giúp mình phần c với nha :v hơi bí phần c
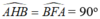
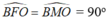
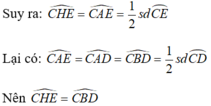
\(\widehat{\text{AFB}}=\widehat{ADB}=90^0\)
Mà ÀB và ADB là hai góc kề cùng nhìn AB dưới hai góc bằng nhau => ÀDB nội tiếp
b) ta có \(\widehat{ACB}=\widehat{AEB}\)( cùng chắn cung AB)
\(\widehat{DFC}=\widehat{BAF}\)( trong tứ giác nội tiếp góc ngaoif tại một đỉnh bằng góc trong đỉnh còn lại )
\(\Rightarrow\widehat{ACB}+\widehat{FDC}=\widehat{BAF}+\widehat{BAE}=90^0\)
\(\Rightarrow DF\perp CA\)
dĐAEDƯÈWEWÈWÉWÈWẺ3GWDFCEWFSCAWECFASEFSAD