Cho hàm số y=2x2.Có đồ thị(P ) . Điểm A thuộc (P ) có hoành độ bằng 1 và điểm B có hoành độ -2. Lập ptrinh đường thẳng d song song với đường thẳng AB tiếp xúc (P)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 10 2021
a: Vì (d) song song với y=2x-3 nên a=2
Vậy: (d): y=2x+b
Thay x=1 và y=1 vào (d), ta được:
b+2=1
hay b=-1
b: Vì (d) song song với y=2x nên a=2
Vậy: (d): y=2x+b
Thay x=-3 và y=0 vào (d), ta được:
b-6=0
hay b=6
7 tháng 1 2022
Đồ thị của hàm số \(y=ax+b\) song song với đường thẳng \(y=3x+1.\) \(\Rightarrow\left\{{}\begin{matrix}a=3.\\b\ne1.\end{matrix}\right.\) (1)
Đồ thị của hàm số \(y=ax+b\) cắt trục hoành tại điểm có hoành độ bằng \(-3.\) \(\Rightarrow\left\{{}\begin{matrix}x=-3.\\y=0.\end{matrix}\right.\) (2)
Thay (1); (2) vào hàm số \(y=ax+b\)\(:0=3.\left(-3\right)+b.\Leftrightarrow b=9\left(TM\right).\)
Vậy hàm số đó là: \(y=3x+9.\)
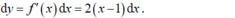
Thay \(x_A=1,x_B=-2\) vào P ta tìm được \(y_A=2,y_{_{ }B}=8\)
Vậy ta tìm được tọa độ giao điểm của \(A\left(1,2\right);B\left(-2,8\right)\)
Phương trình đường thẳng AB có dạng y=ax+b
thay x, y lần lượt vào phương trình đường thẳng AB ta có hệ phương trình
\(\hept{\begin{cases}2=a+b\\8=-2a+b\end{cases}\Leftrightarrow\hept{\begin{cases}a=-2\\b=4\end{cases}}}\)
Vậy phương trình đường thẳng AB có dạng y=-2x+4
vì d song song vói đường thẳng ABnên d có dạng y=-2x+m (\(m\ne4\))
Vì d tiếp xúc với P nên ta có hoành độ giao điểm của d và P là nghiệm của phương trình
\(2x^2+2x-m=0\)*
d tiếp xúc với P nên phương trình * có 1 nghiệm duy nhất hay \(\Delta=4+8m=0\Leftrightarrow m=-\frac{1}{2}\)
Vậy phương trình đường thẳng d có dạng y=-2x-1/2