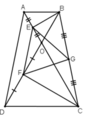
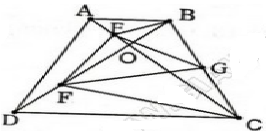
Cho hình thang cân ABCD có góc ACD = 60, O là giao điểm của hai đường chéo. Gọi E, F, G theo thứ tự là trung điểm của OA, OD, BC. Tam giác EFG là tam giác gì ? Vì sao ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 12 2022
Xét ΔOAD có OE/OA=OF/OD
nên EF//AD và EF=AD/2=BC/2
Xét ΔADC và ΔBCD có
AD=BC
DC chung
AC=BD
DO đó: ΔADC=ΔBCD
=>góc ODC=góc OCD=60 đọ
=>ΔODC đều
mà CF là trung tuyến
nên CF vuông góc với BD
ΔBFC vuông tại F
mà FG là trung tuyến
nên FG=BC/2
Xét ΔOAB có góc OBA=góc OAB và góc AOB=60 độ
nên ΔOAB đều
mà BE là trung tuyến
nên BE vuông góc với CE
ΔBEC vuông tại E
mà EG là trung tuyến
nên EG=BC/2
=>EG=EF=FG
=>ΔEFG đều
14 tháng 12 2022
Xét ΔOAD có OE/OA=OF/OD
nên EF//AD và EF=AD/2=BC/2
Xét ΔADC và ΔBCD có
AD=BC
DC chung
AC=BD
DO đó: ΔADC=ΔBCD
=>góc ODC=góc OCD=60 đọ
=>ΔODC đều
mà CF là trung tuyến
nên CF vuông góc với BD
ΔBFC vuông tại F
mà FG là trung tuyến
nên FG=BC/2
Xét ΔOAB có góc OBA=góc OAB và góc AOB=60 độ
nên ΔOAB đều
mà BE là trung tuyến
nên BE vuông góc với CE
ΔBEC vuông tại E
mà EG là trung tuyến
nên EG=BC/2
=>EG=EF=FG
=>ΔEFG đều
14 tháng 12 2022
Xét ΔOAD có OE/OA=OF/OD
nên EF//AD và EF=AD/2=BC/2
Xét ΔADC và ΔBCD có
AD=BC
DC chung
AC=BD
DO đó: ΔADC=ΔBCD
=>góc ODC=góc OCD=60 đọ
=>ΔODC đều
mà CF là trung tuyến
nên CF vuông góc với BD
ΔBFC vuông tại F
mà FG là trung tuyến
nên FG=BC/2
Xét ΔOAB có góc OBA=góc OAB và góc AOB=60 độ
nên ΔOAB đều
mà BE là trung tuyến
nên BE vuông góc với CE
ΔBEC vuông tại E
mà EG là trung tuyến
nên EG=BC/2
=>EG=EF=FG
=>ΔEFG đều
14 tháng 12 2022
Xét ΔOAD có OE/OA=OF/OD
nên EF//AD và EF=AD/2=BC/2
Xét ΔADC và ΔBCD có
AD=BC
DC chung
AC=BD
DO đó: ΔADC=ΔBCD
=>góc ODC=góc OCD=60 đọ
=>ΔODC đều
mà CF là trung tuyến
nên CF vuông góc với BD
ΔBFC vuông tại F
mà FG là trung tuyến
nên FG=BC/2
Xét ΔOAB có góc OBA=góc OAB và góc AOB=60 độ
nên ΔOAB đều
mà BE là trung tuyến
nên BE vuông góc với CE
ΔBEC vuông tại E
mà EG là trung tuyến
nên EG=BC/2
=>EG=EF=FG
=>ΔEFG đều
14 tháng 12 2022
Xét ΔOAD có OE/OA=OF/OD
nên EF//AD và EF=AD/2=BC/2
Xét ΔADC và ΔBCD có
AD=BC
DC chung
AC=BD
DO đó: ΔADC=ΔBCD
=>góc ODC=góc OCD=60 đọ
=>ΔODC đều
mà CF là trung tuyến
nên CF vuông góc với BD
ΔBFC vuông tại F
mà FG là trung tuyến
nên FG=BC/2
Xét ΔOAB có góc OBA=góc OAB và góc AOB=60 độ
nên ΔOAB đều
mà BE là trung tuyến
nên BE vuông góc với CE
ΔBEC vuông tại E
mà EG là trung tuyến
nên EG=BC/2
=>EG=EF=FG
=>ΔEFG đều
14 tháng 12 2022
Xét ΔOAD có OE/OA=OF/OD
nên EF//AD và EF=AD/2=BC/2
Xét ΔADC và ΔBCD có
AD=BC
DC chung
AC=BD
DO đó: ΔADC=ΔBCD
=>góc ODC=góc OCD=60 đọ
=>ΔODC đều
mà CF là trung tuyến
nên CF vuông góc với BD
ΔBFC vuông tại F
mà FG là trung tuyến
nên FG=BC/2
Xét ΔOAB có góc OBA=góc OAB và góc AOB=60 độ
nên ΔOAB đều
mà BE là trung tuyến
nên BE vuông góc với CE
ΔBEC vuông tại E
mà EG là trung tuyến
nên EG=BC/2
=>EG=EF=FG
=>ΔEFG đều
1 tháng 1 2018
Xét ∆ OAD có: OE=AE; OE=FD => EF là đtb của ∆ OAD => EF=1/2AD=1/2BC (1) và EF//AD
Ta có ABCD là hình thang cân => OCDˆ=ODCˆOCD^=ODC^=60 độ ( tự lập luận)
=> ∆ ODC đều có CF là đường trung tuyến đồng thời là đường cao => CF⊥⊥BD
∆BFC vuông tại F có FG là đường trung tuyến => FG=BG=CG=BC/2( theo t/c đường trung tuyến trong ∆ vuông) (2)
Chứng minh tương tự: EG=BC/2 (3)
Từ (1) ; (2) và (3) => FG=EF=EG => ∆ EFG đều
Nhấn đúng cho mình nha ^3^
1 tháng 1 2018
Đây là câu trả lời đầy đủ của mình
Hãy ấn đúng cho mình nha các bạn ^3^
CM
3 tháng 3 2019
ΔAOB đều ⇒ BE là đường trung tuyến đồng thời là đường cao
⇒ BE ⊥ AO
⇒ ΔBEC vuông tại E
Mà EG là đường trung tuyến
⇒ 
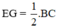(1)
ΔCOD đều ⇒ CF là đường trung tuyến đồng thời là đường cao
⇒ CF ⊥ OD
⇒ ΔBFC vuông tại F
Mà FG là đường trung tuyến
⇒ 
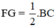(2)
Hình thang ABCD (AB// CD) có: AC = AO + OC = OB + OD = BD
⇒ ABCD là hình thang cân
⇒ AD = BC.
ΔAOD có: AE = EO, FO = FD
⇒ EF là đường trung bình của ΔAOD
⇒ 
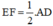
Mà AD = BC (cmt)
⇒ 
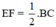(3)
Từ (1); (2); (3) suy ra EF = FG = GE ⇒ ΔEFG đều (đpcm).
Trả lời
Xét tam giác OAD ta có: OE=AE; OE=FD \(\Rightarrow\)EF là ĐTB của tam giác OAD
\(\Rightarrow EF=\frac{1}{2}AD=\frac{1}{2}BC\left(1\right)\)và EF//AD
Ta có tam giác ABCD là tâm giác cân \(\Rightarrow\widehat{OCD}\)\(=\widehat{ODC}\)=\(60^0\)(tự lập luận)
Ta có: Tam giác ODC đều có CF là đường trung tuyến đồng thời là đường cao
\(\Rightarrow CF\perp BD\)
Tam giác BFC vuông tại F có FG là đường trung tuyến
\(\Rightarrow FG=CG=BG=\frac{BC}{2}\)(Theo t/c đường trung tuyến trong \(\Delta\)vuông)(2)
Chứng minh tường tự: EG=\(\frac{BC}{2}\left(3\right)\)
\(\left(1\right)\left(2\right)\left(3\right)\Rightarrow FG=EF=EG\Rightarrow\Delta EFG\)là tam giác đều
Em cop mạng hay ghê không 1 chút sửa đổi a thánh phcuj