Question

[Đậu Đình Kiên]

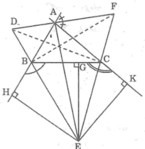
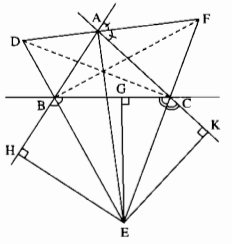
Cho tam giác ABC Các đường phân giác của các góc ngoài đỉnh B và đỉnh C cắt nhau ở E gọi G H K theo thứ tự là chân đường vuông góc kẻ từ A đến các đoàn BC AB AC

a) có nhận xét gì về độ dài các đoạn EH EG EK 

b) Chứng minh AE là tia phân giác của góc B AC

c) đường phân giác góc ngoài đỉnh A của tam giác ABC cắt các đường thẳng BE CE tại D và F Chứng minh AE vuông góc với DF

d các đường thẳng AE BF CD là các đường gì trong tam giác ABC

e các đường thẳng AE FB CD là các đường gì trong tam giác DEF

Answer 1

[Aug.21]

a) E thuộc tia phân giác của \(\widehat{CBH}\)

\(\Rightarrow\)EG = EH (tính chất tia phân giác)          (1)

E thuộc tia phân giác của \(\widehat{BCK}\)

\(\Rightarrow\)EG = EK (tính chất tia phân giác)           (2)

Từ (1) và (2) suy ra:  EH = EG = EK

b) EH = EK

\(\Rightarrow\)E thuộc tia phân giác của \(\widehat{BAC}\)mà E khác A

 Vậy AE là tia phân giác của \(\widehat{BAC}\)

c) AE  là tia phân giác góc trong tại đỉnh A.

    AF là tia phân giác góc ngoài tại đỉnh A.

\(\Rightarrow AE\perp AF\) (tính chất hai góc kề bù)

Hay \(AE\perp DF\)

d) Chứng minh tương tự câu a ta có BF là tia phân giác của \(\widehat{ABC}\)

CD là tia phân giác của \(\widehat{ACB}\)

Vậy các đường AE, BF, CD là các đường phân giác của ∆ABC

e) BF là phân giác góc trong tại đỉnh B.

      BE là phân giác góc ngoài tại đỉnh B.

\(\Rightarrow BF\perp BE\) (tính chất hai góc kề bù)

Hay \(BF\perp ED\)

CD là đường phân giác góc trong tại C

CE là đường phân giác góc ngoài tại C

\(\Rightarrow CD\perp CE\)(tính chất hai góc kề bù)

Hay \(CD\perp EF\)

Các đường thẳng AE, FB, DC là các đường cao trong tam giác DEF.