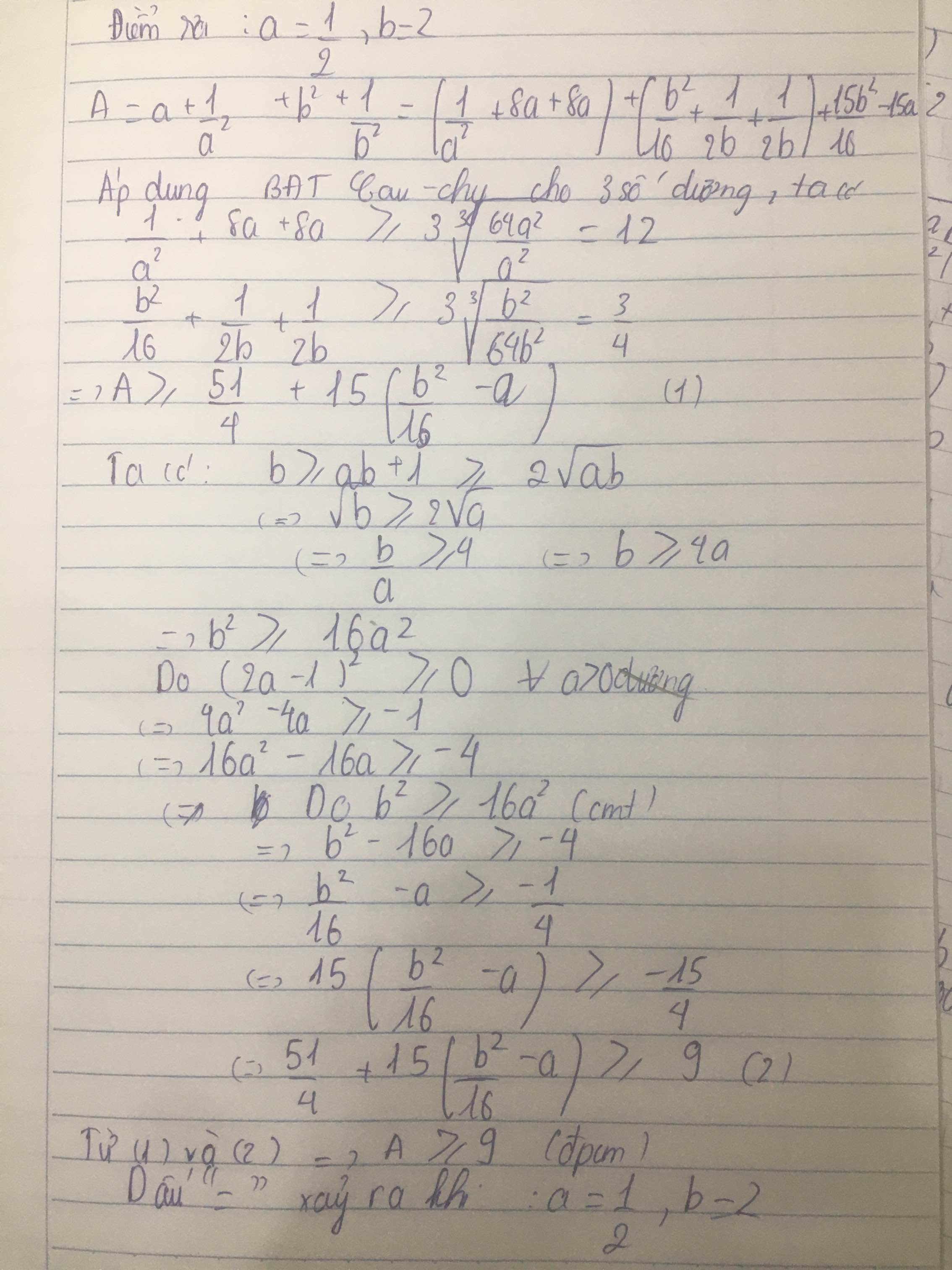Cho a,b,c là các số lớn hơn hoặc bằng 0 và nhỏ hơn hoặc bằng 2 thỏa mãn a+b+c=3 chứng minh a^2+b^2+c^2 nhỏ hơn hoặc bằng 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 2 2018
bài 1:
a, -9 \(\le\)x\(\le\)8
\(\Rightarrow\)x \(\in\){-9, -8, -7, ..., -1, 0, 1, 2,,...., 8}
tổng các giá trị của x là: (-9) + (-8) + (-7 )+ ... + (-1 )+ 0 + 1 +2 +....+ 8
= (-9) + [(-8) +8] + [(-7 ) + 7] + ....+ [ -1 +1] +0
= -9 +0+0+0....+0
= -9
các câu sau làm tương tự
bài 2 ;
các câu a, b tương tự.
c, |x|< 7
suy ra - 7 < x< 7
làm tương tự
MH
30 tháng 3 2022
a) Áp dụng BĐT Svácxơ, ta có:
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{\left(1+1+1\right)^2}{a+b+c}=\dfrac{9}{6}=\dfrac{3}{2}\)
Dấu "=" \(\Leftrightarrow a=b=c=2\)
C6. Cho các số thực dương thoả mãn: ab+1 nhỏ hơn hoặc bằng b Chứng minh rằng : ( a + (1/a^2) ) + ( b^2 + (1/b) ) lớn hơn hoặc bằng 9
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2022
\(ab+1\le b\Rightarrow a+\dfrac{1}{b}\le1\)
Đặt \(\left(a;\dfrac{1}{b}\right)=\left(x;y\right)\Rightarrow x+y\le1\)
Gọi vế trái của BĐT cần chứng minh là P:
\(P=x+\dfrac{1}{x^2}+y+\dfrac{1}{y^2}=\left(\dfrac{1}{x^2}+8x+8x\right)+\left(\dfrac{1}{y^2}+8y+8y\right)-15\left(x+y\right)\)
\(P\ge3\sqrt[3]{\dfrac{64x^2}{x^2}}+3\sqrt[3]{\dfrac{64y^2}{y^2}}-15.1=9\) (đpcm)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(\dfrac{1}{2};\dfrac{1}{2}\right)\) hay \(\left(a;b\right)=\left(\dfrac{1}{2};2\right)\)
30 tháng 12 2019
tham khảo thôi nhé ko giống y sì đâu
https://olm.vn/hoi-dap/detail/213882782299.html
