Bài 4: Tìm X: (1 điểm) (M4)
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 1: Ta có: \(4\dfrac{3}{5}+\dfrac{7}{10}< X< \dfrac{20}{3}\)
\(\dfrac{23}{5}+\dfrac{7}{10}< X< \dfrac{20}{3}\)
\(\dfrac{138}{30}< X< \dfrac{200}{3}\)
\(\Rightarrow X\in\left\{\dfrac{160}{30};\dfrac{161}{30};\dfrac{162}{30};...;\dfrac{198}{30};\dfrac{199}{30}\right\}\)
Bài 2: \(X-2019\dfrac{2}{13}=3\dfrac{7}{26}+4\dfrac{7}{52}\)
\(\Rightarrow X-\dfrac{26249}{13}=\dfrac{85}{26}+\dfrac{215}{52}\)
\(\Rightarrow X-\dfrac{26249}{13}=\dfrac{385}{52}\)
\(\Rightarrow X=\dfrac{105381}{52}\)

Đáp án là B
Ta có: y ' = 4 x 3 − 4 m x , y '' = 12 x 2 − 4 m .
Hàm số đã cho đạt cực tiểu tại x = − 1 nên y ' − 1 = 0 y ' ' − 1 > 0 ⇒ − 4 + 4 m = 0 12 + 4 m > 0 ⇔ m = 1.

Đáp án C.
Ta có y’ = 4x3 – 4mx; y’’ = 12x2 – 4m.
Để hàm số đạt cực tiểu tại x = -1 thì y’(-1) = 0 ó -4 + 4m = 0 ó m = 1
Khi m = 1 thì y’’(-1) = 12 – 4m = 12 – 4.1 = 8 > 0 => hàm số đạt cực tiểu tại x = -1.
Vậy m = 1 là giá trị cần tìm

Ta có:
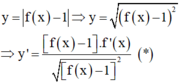
Do pt có 3 điểm cực trị ( vì ab< 0) nên phương trình f’ ( x) =0 có 3 nghiệm phân biệt.
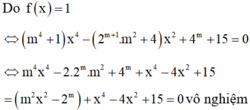
Do đó (*) có 3 nghiệm phân biệt.
Chọn C.

Chọn A
y ' = y = 4 x 3 - 4 m 2 x
Hàm số có 3 điểm cực trị khi m ≠ 0
Khi đó 3 điểm cực trị là
![]()
Gọi I là tâm đường tròn ngoại tiếp( nếu có) của tứ giác ABOC .
Do tính chất đối xứng , ta có
A,O,I thẳng hàng
⇒ A O là đường kính của đường tròn ngoại tiếp( nếu có) của tứ giác ABOC
![]()
![]()
Kết hợp điều kiện m = ± 1 ( thỏa mãn)

BÀI 1:
a) \(17.2-17.102\)
\(=17.\left(2-102\right)\)
\(=17.\left(-100\right)\)
\(=-1700\)
b) \(45-9\left(13+5\right)\)
\(=45-9.13-9.5\)
\(=-9.13=-117\)
Baì 1:
a.\(17\times2-17\times102\)
\(=17\left(2-102\right)\)
\(=17\times\left(-100\right)\)
\(=-1700\)
b.\(45-9\left(13+5\right)\)
\(=45-9\times18\)
\(=45-162\)
\(=-117\)
Bài 2: Theo thứ tự giảm dần: \(318;213;112;35;22\)
Bài 3:
a. \(2x-35=15\)
\(2x=15+35\)
\(2x=50\)
\(x=50\div2\)
\(x=25\)
b.\(15-\left(x-7\right)=-21\)
\(x-7=15-\left(-21\right)\)
\(x-7=36\)
\(x=36+7\)
\(x=43\)
bạn phải ghi phép tính thì mới làm được chứ
mình xin lôi