Hai tiếp tuyến A,B của đường tròn (O;R) cắt nhau tại M. Biết OM = 2R. Tính số đo góc ở tâm AOB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 6 2023
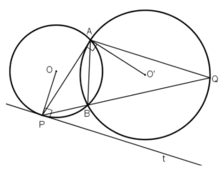
2: góc OME+góc OAE=180 độ
=>OMEA nội tiếp
=>góc AOE=góc AME=góc OMB
CM
22 tháng 1 2019
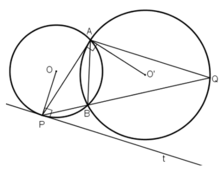
Kiến thức áp dụng
Trong một đường tròn:
+ Số đo của góc nội tiếp bằng một nửa số đo của cung bị chắn.
+ Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.
11 tháng 4 2017
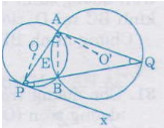
Nối AB. Ta có: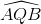 
= 
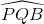(1)
( cùng chắn cung và có số đo bằng 
sđ
)
= 
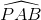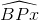(2)
(cùng chắn cung nhỏ 
và có số đo bằng sđ
)
TỪ (1) và (2) có 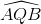= 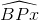từ đó AQ // Px (có hai góc so le trong bằng nhau)
CM
9 tháng 5 2019
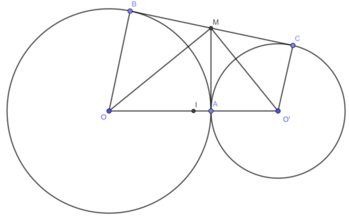
Ta có:
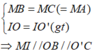
Mà OB ⊥ BC ⇒ IM ⊥ BC
Ta có:
IM ⊥ BC
BC ⋂ (I; IM) = {M}
Suy ra, BC là tiếp tuyến của đường tròn tâm I, bán kính IM
13 tháng 3 2023
Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC tại H
=>AH*AO=AB^2
Xet ΔABD và ΔAEB có
góc ABD=góc AEB
góc BAD chung
=>ΔABD đồng dạng với ΔAEB
=>AB^2=AD*AE=AH*AO
=>AD/AO=AH/AE
=>ΔADH đồng dạng với ΔAOE
=>góc ADH=góc AOE
=>góc DHO+góc DEO=180 độ
=>DEOH nội tiếp
=>góc EHO=góc EDO
