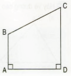
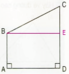
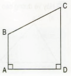
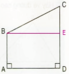
Cho hình vuông ABCD , E là điểm trên cạnh DC ;F là điểm trên tia đối của tia bc sao cho BF=DE.
a/ Chứng minh tam giác AEF vuông cân .
b/Gọi i là trung điểm EF . Chứng minh i thuộc BD
c/ Lấy K đối xứng với A qua i . Chứng minh tứ giác AEKF là hinh vuông .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

MH
8 tháng 11 2021
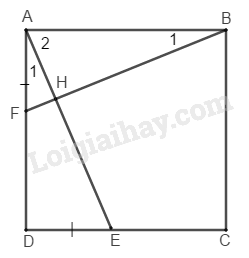
Xét ΔABF và ΔDAE ta có:
AB=DA (gt)
ˆBAF=ˆADE=900
AF=DE (gt)
Do đó: ΔABF=ΔDAE(c.g.c)
⇒BF=AE và ˆB1=ˆA1
Gọi H là giao điểm của AE và BF
ˆBAF=ˆA1+ˆA2=900
⇒ ˆB1+ˆA2=900
Trong ΔABH ta có:
ˆAHB+ˆB1+ˆA2=1800
ˆAHB=1800−(ˆB1+ˆA2)=1800−900=900
Vậy AE⊥BF