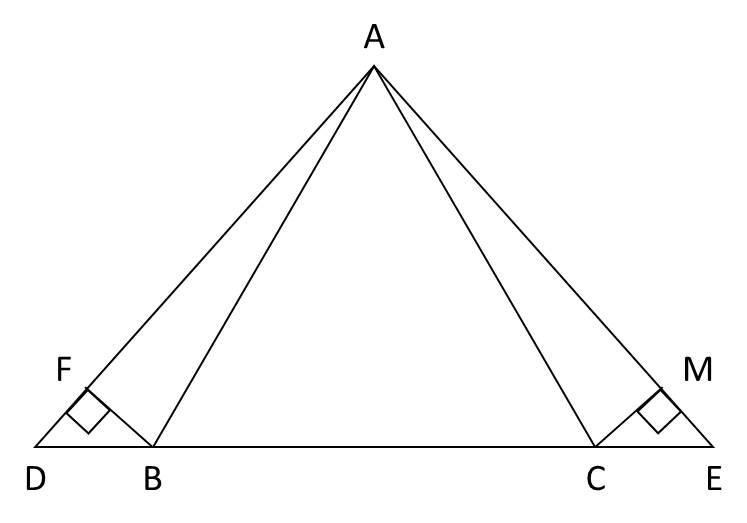
Cho tam giác AED vông cân tại A .Trên tia đối cảu tia EA và DA lần lượt lấy C ;B ( ED=DB).Đường thẳng đi qua A vông góc với CD cắt CD tại G.Đường thẳng đi qua E vông góc với CD cắt CB ở H và cắt AB ở M Qua A kẻ đg thg // BC cắt MH tại I . Chứng minh:
a. Tam giác ACD=tg AME
b. Tg AGB=tg MIA
c. BC=GH
d. Tg MCB là tg j ??
Giúp với😣😣