Vẽ tam giác ABC có độ dài các cạnh là:AB=4cm;AC=8cm và AD là đường phân giác của góc A.
Tính tỉ số diện tích của tam giác ABD và diện tích của tam giác ACD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 9 2018
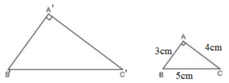
Xét ΔABC có: AB2 + AC2 = 32 + 42 = 25 = 52 = BC2
⇒ ΔABC vuông tại A (Định lý Pytago đảo)
⇒ Diện tích tam giác ABC bằng:
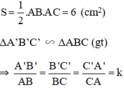
(với k là tỉ số đồng dạng).
Lại có tỉ số diện tích bằng bình phương tỉ số đồng dạng
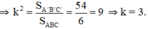
⇒ A’B’ = 3.AB = 3.3 = 9 (cm)
B’C’ = 3.BC = 3.5 = 15 (cm)
C’A’ = 3.CA = 3.4 = 12 (cm)
Vậy độ dài ba cạnh của tam giác lần lượt là 9cm, 12cm, 15cm.
11 tháng 1 2018
Theo bài ra ta có: Độ dài các cạnh góc vuông tỉ lệ với 3 và 4. Nên ta có:
\(\frac{AB}{3}=\frac{AC}{4}\) \(\Rightarrow\left(\frac{AB}{3}\right)^2=\left(\frac{AC}{4}\right)^2\) \(\Rightarrow\frac{AB^2}{9}=\frac{AC^2}{16}\)
Theo định lí Py-ta-go, tam giác vuông ABC có cạnh huyền BC \(\Rightarrow AB^2+AC^2=BC^2=4^2=16\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta được:
\(\frac{AB^2}{9}=\frac{AC^2}{16}=\frac{AB^2+AC^2}{9+16}=\frac{16}{25}\)
\(\Rightarrow\frac{AB^2}{9}=\frac{16}{25}\Rightarrow AB^2=5,76\Rightarrow AB=2,4\left(cm\right)\)
\(\frac{AC^2}{16}=\frac{16}{25}\Rightarrow AC^2=10,24\Rightarrow AC=3,2\left(cm\right)\)
Vậy AB = 2,4 cm
AC = 3,2 cm
BC = 4 cm
PN
2
KC
23 tháng 7 2021
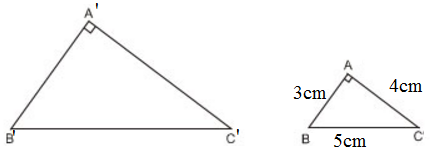
Xét ΔABC có:
ˆA=ˆB+ˆC=60o+30o=90o
⇒ΔABC vuông tại A
Có AB là góc đối diện với ˆC=30o
⇒AB=12BC=12.4=2(cm)
Vậy AB=2cm
HT
3
1 tháng 5 2017
Ta có \(AB^2+AC^2=3^2+4^2=25\)
\(BC^2=5^2=25\)
\(\Rightarrow AB^2+AC^2=BC^2\)Áp dụng pi- ta - go đảo ta có :
\(\Delta ABC\)vuông tại A
\(\Rightarrow\widehat{BAC}=90^o\)
1 tháng 5 2017
NHẬN XÉT \(AB^2+AC^2=3^2+4^2=25=5^2=BC^2\)
Nên áp dụng định lý Pytago đảo ta có tam giác ABC vuông tại A
Vậy góc BAC bằng \(90^o\)
\(\dfrac{S_{ABD}}{S_{ACD}}=\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{4}{8}=\dfrac{1}{2}\)