Cho tam giác ABC vuông tại A,vẽ đường cao AH.ChoAB=6cm;AC=8cm
a/ Chứng minh ΔHBA đồng dạng ΔABC
b/ Tính BC,AH,BH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 3 2023
a: Xét ΔABC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
Xét ΔABD vuông tại D và ΔCAD vuông tại D có
góc DBA=góc DAC
=>ΔABD đồng dạng với ΔCAD
b: góc EAF+góc EDF=180 độ
=>AFDE nội tiếp
=>góc AFD+góc AED=180 độ
=>góc AFD=góc CED
CM
1 tháng 4 2019
Xét ∆ ABC vuông tại A ta có:
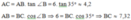
Vì ∆ ABC vuông tại A ta có:
Đáp án cần chọn là: C
3 tháng 9 2021
a: Ta có: ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=60^0\)
Xét ΔABC vuông tại A có
\(AC=AB\cdot\tan30^0\)
\(=2\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow BC=4\sqrt{3}\left(cm\right)\)
D
18 tháng 1 2022
a. Xét tam giác ABC vuông tại A có:
AB2+AC2=BC2 (định lý Py-ta-go)
=>62+AC2=BC2
=>AC=8 cm.
=> SABC=AB.AC=6.8=48 (cm)
b. Ta có: SABC=AB.AC=BC.AH
=>6.8=10.AH
=>AH=4,8 cm.
18 tháng 1 2022
a/
diện tích tam giác ABC là:
\(\dfrac{6.10}{2}\)=30 (cm2)
đường cao AH là
30:10=3 cm
18 tháng 3 2023
a: Xet ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
AH=6*8/10=4,8cm
BH=6^2/10=3,6cm
28 tháng 6 2023
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
góc HBA=góc HAC
=>ΔHBA đồng dạng với ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC
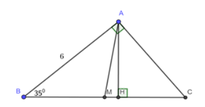
a.
Xét hai tam giác vuông HBA và ABC có:
\(\left\{{}\begin{matrix}\widehat{HBA}\text{ chung}\\\widehat{AHB}=\widehat{BAC}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta HBA\sim\Delta ABC\left(g.g\right)\)
b.
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Do \(\Delta HBA\sim\Delta ABC\left(cmt\right)\Rightarrow\dfrac{AH}{AC}=\dfrac{AB}{BC}\)
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4,8\left(cm\right)\)
Áp dụng định lý Pitago trong tam giác vuông HBA:
\(BH=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=3,6\left(cm\right)\)