Trong không gian với hệ tọa độ Oxyz, cho hình chóp có đỉnh S(2;3;5) và đáy là một đa giác nằm trong mặt phẳng P : 2 x + y − 2 z − 3 = 0 , có diện tích bằng 12. Tính thể tích của khối chóp đó.
A. 4
B. 24
C. 8
D. 72
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
1 tháng 9 2019
Đúng(0)
Những câu hỏi liên quan
CM
1 tháng 12 2018
Đáp án C.
Chiều cao của khối chóp có độ dài bằng d S , P = 2 .
Suy ra thể tích khối chóp đã cho là V = 1 3 . 12 . 2 = 8 .
CM
29 tháng 3 2019
Chọn đáp án A
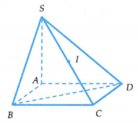
Lấy điểm C trong mặt phẳng (ABD) sao cho ABCD là hình chữ nhật
Do vậy, tâm mặt cầu ngoại tiếp hình chóp là trung điểm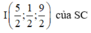 
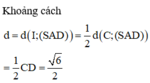
Cách 2: Gọi I(a;b;c) là tâm mặt cầu ngoại tiếp hình chóp là trung điểm S.ABCD. Ta có:
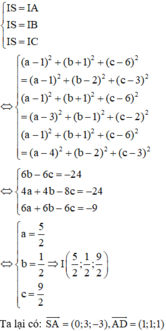
STUDY TIP |
Khi xác định tâm mặt cầu ngoại tiếp hình chop hoặc lăng trụ ta có thể làm theo hai hường: + Hướng 1: Dùng điều kiện tâm cách đều các đỉnh đi đến giải hệ phương trình + Hướng 2: Dựa vào tính đặc biệt của hình như: Hình chop đều, hình chop có các đỉnh cùng nhìn một cạnh dưới một góc vuông |
