Trong mặt phẳng Oxy, cho điểm I(-1;1) và đường thẳng d: x+y+2=0.Viết phương trình đường tròn tâm I cắt d tại hai điểm phân biệt A,B sao cho AB=2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 1 2022
\(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=\dfrac{-1+3}{2}=1\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{5+\left(-1\right)}{2}=2\end{matrix}\right.\)
\(\Rightarrow I\left(1;2\right)\)
27 tháng 3 2022
gọi H là trung điểm AB
=>IH⊥AB
=>\(d_{\left(I,d\right)}=\dfrac{\left|1\cdot1-1\cdot1+2\right|}{\sqrt{1^2+\left(-1\right)^2}}=\sqrt{2}\)
=>IH=\(\sqrt{2}\)
Mà HB=\(\dfrac{AB}{2}\)=1
Xét ΔIHB vuông tại H có:
IB=\(\sqrt{IH^2+HB^2}=\sqrt{2+1}=\sqrt{3}\)
=>R=\(\sqrt{3}\)
Vậy đường tròn tâm I (1; -1); R=\(\sqrt{3}\) là:
(x-1)2+(y+1)2=3
27 tháng 3 2022
REFER
https://hoc24.vn/index.php/cau-hoi/trong-mat-phang-oxy-cho-diem-i-1-1-va-duong-thang-d-xy20-viet-phuong-trinh-duong-tron-tam-i-cat-d-tai-hai-diem-ab-sao-cho-ab2.5543217878093
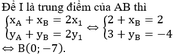
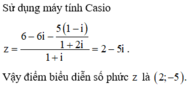
\(d\left(I;d\right)=\dfrac{\left|-1+1+2\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\)
Gọi H là trung điểm AB \(\Rightarrow IH\perp AB\Rightarrow IH=d\left(I;d\right)=\sqrt{2}\)
Áp dụng định lý Pitago:
\(R^2=IA^2=IH^2+AH^2=IH^2+\left(\dfrac{AB}{2}\right)^2=3\)
Phương trình đường tròn: \(\left(x+1\right)^2+\left(y-1\right)^2=3\)