Tìm giá trị nguyên của m để phương trình có đúng 3 nghiệm thuộc \(\left[-3;0\right]\)
\(2\left(x^2+2x\right)^2-\left(4m-3\right)\left(x^2+2x\right)+1-2m=0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2020
\(\Leftrightarrow\left(cosx+1\right)\left(4cos2x-m.cosx\right)=m\left(1-cosx\right)\left(1+cosx\right)\)
\(\Leftrightarrow4cos2x-m.cosx=m\left(1-cosx\right)\)
\(\Leftrightarrow4cos2x=m\)
\(\Rightarrow cos2x=\dfrac{m}{4}\)
Pt có đúng 2 nghiệm thuộc đoạn đã cho khi và chỉ khi:
\(-1< \dfrac{m}{4}\le-\dfrac{1}{2}\Leftrightarrow-4< m\le-2\)
Có 2 giá trị nguyên của m thỏa mãn
HP
1 tháng 8 2021
1.
\(cos2x-3cosx+2=0\)
\(\Leftrightarrow2cos^2x-3cosx+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pm\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(x=k2\pi\in\left[\dfrac{\pi}{4};\dfrac{7\pi}{4}\right]\Rightarrow\) không có nghiệm x thuộc đoạn
\(x=\pm\dfrac{\pi}{3}+k2\pi\in\left[\dfrac{\pi}{4};\dfrac{7\pi}{4}\right]\Rightarrow x_1=\dfrac{\pi}{3};x_2=\dfrac{5\pi}{3}\)
\(\Rightarrow P=x_1.x_2=\dfrac{5\pi^2}{9}\)
HP
1 tháng 8 2021
2.
\(pt\Leftrightarrow\left(cos3x-m+2\right)\left(2cos3x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos3x=\dfrac{1}{2}\left(1\right)\\cos3x=m-2\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow x=\pm\dfrac{\pi}{9}+\dfrac{k2\pi}{3}\)
Ta có: \(x=\pm\dfrac{\pi}{9}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=\pm\dfrac{\pi}{9}\)
Yêu cầu bài toán thỏa mãn khi \(\left(2\right)\) có nghiệm duy nhất thuộc \(\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}m-2=0\\m-2=1\\m-2=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=2\\m=3\\m=1\end{matrix}\right.\)
TH1: \(m=2\)
\(\left(2\right)\Leftrightarrow cos3x=0\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=\dfrac{\pi}{6}\left(tm\right)\)
\(\Rightarrow m=2\) thỏa mãn yêu cầu bài toán
TH2: \(m=3\)
\(\left(2\right)\Leftrightarrow cos3x=0\Leftrightarrow x=\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=0\left(tm\right)\)
\(\Rightarrow m=3\) thỏa mãn yêu cầu bài toán
TH3: \(m=1\)
\(\left(2\right)\Leftrightarrow cos3x=-1\Leftrightarrow x=\dfrac{\pi}{3}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow\left[{}\begin{matrix}x=\pm\dfrac{1}{3}\\x=-1\\x=-\dfrac{5}{3}\end{matrix}\right.\)
\(\Rightarrow m=2\) không thỏa mãn yêu cầu bài toán
Vậy \(m=2;m=3\)
CM
6 tháng 12 2017
Chọn D
Bảng biến thiên
Dựa vào bảng biến thiên suy ra phương trình có nghiệm khi
CM
14 tháng 2 2017
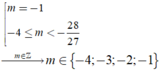
Ta có: Δ = 4 m − 1 2 − 4.2. 2 m − 1 = 4 m − 3 2
2 x 2 + 2 x 2 − 4 m − 1 x 2 + 2 x + 2 m − 1 = 0
⇔ x 2 + 2 x = 1 2 ( 1 ) x 2 + 2 x = 2 m − 1 ( 2 )
( 1 ) ⇔ x 2 + 2 x − 1 2 = 0 ⇔ x = − 2 + 6 2 ∉ − 3 ; 0 x = − 2 − 6 2 ∈ − 3 ; 0
Do đó (1) chỉ có 1 nghiệm thuộc − 3 ; 0
Để phương trình đã cho có 3 nghiệm thuộc đoạn − 3 ; 0 thì phương trình (2) phải có hai nghiệm phân biệt thuộc đoạn và hai nghiệm này phải khác − 2 − 6 2
2 ⇔ x + 1 2 = 2 m
Phương trình (2) có hai nghiệm phân biệt khác − 2 − 6 2 và thuộc đoạn − 3 ; 0
⇔ 2 m > 0 − 2 − 6 2 + 1 2 ≠ 2 m − 3 ≤ − 1 + 2 m ≤ 0 − 3 ≤ − 1 − 2 m ≤ 0 ⇔ m > 0 m ≠ 3 4 m ≤ 1 2 m ≤ 2
Không có giá trị nào của m thỏa mãn.
Đáp án cần chọn là: D
CM
12 tháng 10 2018
Đáp án D
⇔ 1 + cos x cos 4 x − m cos x − m + m cos x = 0
⇔ 1 + cos x cos 4 x − m = 0 ⇔ cos x = − 1 1 cos 4 x = m 2 1 ⇔ x = π + k 2 π k ∈ ℤ ; x = π + k 2 π ∈ 0 ; 2 π 3 ⇒ k ∈ ∅
16 tháng 5 2021
1) điều kiện của m: m khác 5/2
thế x=2 vào pt1 ta đc:
(2m-5)*4 - 4(m-1)+3=0 <=> 8m-20-4m+4+3=0<=> 4m = 13 <=> m=13/4 (nhận)
lập △'=[-(m-1)]2-*(2m-5)*3 = (m-4)2
vì (m-4)2 ≥ 0 nên phương trình có nghiệm kép => x1= x2 =2
3) vì △'≥0 với mọi m nên phương trình đã cho có nghiệm với mọi m
