Cho tam giác ABC . Trên AB lấy điểm M sao cho AB gấp đôi AM ; trên BC lấy điểm N sao cho BN = 3/2 NC . Các đoạn thẳng AN và CM cắt nhau ở I. Nối Bvới I .
a)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 5 2022
Kẻ ND//AB (D thuộc AB).
Có: \(MC=\dfrac{1}{2}AM;MC+AM=AC\)
\(\Rightarrow\dfrac{AM}{AC}=\dfrac{2}{3};\dfrac{MC}{AC}=\dfrac{1}{3}\).
Có: \(NC=2BN;NC+BN=BC\)
\(\Rightarrow\dfrac{NC}{BC}=\dfrac{2}{3};\dfrac{BN}{BC}=\dfrac{1}{3}\)
△ABC có: ND//AB.
\(\Rightarrow\dfrac{ND}{AB}=\dfrac{DC}{AB}=\dfrac{2}{3}\) (định lí Ta-let)
\(\Rightarrow ND=\dfrac{2}{3}AB=\dfrac{2}{3}.6=4\left(cm\right)\).
\(\dfrac{AD}{AC}=\dfrac{BN}{BC}=\dfrac{1}{3}=\dfrac{MC}{AC}\Rightarrow AD=MC=\dfrac{1}{3}AC\)
Mà \(AD+DM+MC=AC\Rightarrow AD=DM=MC=\dfrac{1}{3}AC\); \(AM=DC=\dfrac{2}{3}AC\).
\(\Rightarrow\dfrac{MD}{AM}=\dfrac{1}{2}\)
△APM có: DN//AP.
\(\Rightarrow\dfrac{ND}{AP}=\dfrac{MD}{AM}=\dfrac{1}{2}\) (hệ quả định lí Ta-let)
\(\Rightarrow AP=2ND=2.4=8\left(cm\right)\)
14 tháng 3 2023
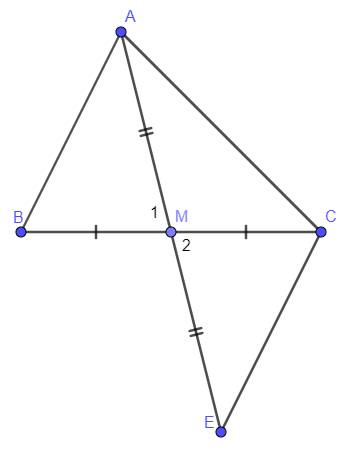
Có `M` là tđ `BC=>BM=CM`
Xét `Delta MAB` và `Delta MEC` có :
`{:(MA=ME(GT)),(hat(M_1)=hat(M_2)(đối.đỉnh)),(BM=CM(cmt)):}}`
`=>Delta MAB=Delta MEC(c.g.c)(đpcm)`
8 tháng 3 2017
SABCD=1/2(AB+CD)xAH
AB+CD=2xSABCD/AH
=2x36,75/4,2=17,5
mà CD-AB=7,5
CD=12,5;AB=5
Ta có : SADC=1/2AHxCD=1/2x4,2x12,5=26,25
Xét SABC=1/2AHxAB=1/2x4,2x5=10,5
Xét tam giác CAE và tam giác CAD chung đường cao kẻ từ C
Cạnh đáy AE=2/3AD(do AD=3/5DE)
SAEC=2/3SADC=2/3x26,25=17,5
Ta có SAEC - SABC = 17,5-10,5=7dm2
Đáp số : 7 dm2
