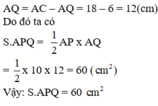Câu 4 : Cho hình tam giác ABC có góc A là góc vuông có AB = 15cm

TH

Trần Hồng Hạnh

14 tháng 5 2023

Câu 4 : Cho hình tam giác ABC có góc A là góc vuông có AB = 15cm ; AC có độ dài bằng 6/5 độ dài cạnh AB ; P là một điểm AB sao cho AP . Trên cạnh AC lấy điểm Q sao cho CQ = 1/3 CA. A, Tính diện tích tam giác ABC. B, Tính diện tích tam giác CPB. C, Tính diện tích tam giác BAQ. D, Tính diện tích tứ giác...

Đọc tiếp

#Toán lớp 6

0

VT

Vũ Thị Thanh Thảo

8 tháng 1 2016 - olm

Cho hình tam giác vuông ABC có hai cạnh góc vuông Ab=15cm, AC=2dm. Tính diện tích hình tam giác vuông ABC

#Toán lớp 5

0

VT

Vũ Thị Thanh Thảo

8 tháng 1 2016 - olm

Cho tam giác vuông ABC có hai cạnh góc vuông AB=15cm, AC=2dm. Tính diện tích hình tam giác vuông ABC

#Toán lớp 5

0

HL

hoa ly hong

5 tháng 1 2016 - olm

Cho hình tam giác vuông ABC có hai cạnh góc vuông AB = 15cm , AC = 2dm . Tính diện tích tam giác vuông ABC

#Toán lớp 5

6

TT

Trần Trương Quỳnh Hoa

5 tháng 1 2016

2dm=20cm

Cạnh AB là chiều cao

Cạnh AC là cạnh đáy

Diện tích hình tam giác ABC là

\(\frac{15x20}{2}=150\left(cm2\right)\)

Đúng(0)

ND

Nguyễn Đức Huy

5 tháng 1 2016

2dm = 20cm

Diện tích hình tam giác vuông ABC là : 15 x 20 : 2 = 150 (cm2)

Đáp số : 150cm2

Đúng(0)

NB

Nguyễn Bảo Lâm 7/5

28 tháng 3 2023

Cho tam giác ABC vuông tại A, kẻ đường cao AH

a) tam giác AHB và tam giác CAB có đồng dạng với nhau không? Vì sao?

b) Cho AB=15cm, AC=20cm. Tính HB?

c) kẻ HD vuông góc với AB và HE vuông góc. Chứng minh AD.AB= AE.AC

làm câu C cho mình là đc rồi nha

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

28 tháng 3 2023

a: Xét ΔAHB vuông tại H và ΔCAB vuông tại A có

góc B chung

=>ΔAHB đồng dạng với ΔCAB

b: \(BC=\sqrt{15^2+20^2}=25\left(cm\right)\)

HB=15^2/20=9cm

c: AD*AB=AH^2

AE*AC=AH^2

=>AD*AB=AE*AC

Đúng(1)

PT

Pham Trong Bach

16 tháng 5 2018

Cho hình tam giác ABC có góc A là góc vuông. AB = 15cm; AC = 18cm; P là một điểm nằm trên cạnh AB sao cho AP = 10cm. Qua điểm P, kẻ đường thẳng song song với cạnh BC, cắt cạnh AC tại Q.Tính diện tích của hình tam giác APQ.

#Toán lớp 5

1

CM

Cao Minh Tâm

16 tháng 5 2018

Đúng(0)

PT

Pham Trong Bach

21 tháng 9 2019

Cho hình tam giác ABC có góc A là góc vuông. AB = 15cm; AC = 18cm; P là một điểm nằm trên cạnh AB sao cho AP = 10cm. Qua điểm P, kẻ đường thẳng song song với cạnh BC, cắt cạnh AC tại Q.Tính diện tích của hình tam giác APQ.

#Toán lớp 5

1

CM

Cao Minh Tâm

21 tháng 9 2019

Đúng(1)

PT

Pham Trong Bach

19 tháng 4 2017

Cho hình tam giác ABC có góc A là góc vuông. AB = 15cm; AC = 18cm; P là một điểm nằm trên cạnh AB sao cho AP = 10cm. Qua điểm P, kẻ đường thẳng song song với cạnh BC, cắt cạnh AC tại Q.Tính diện tích của hình tam giác APQ.

#Toán lớp 5

1

CM

Cao Minh Tâm

19 tháng 4 2017

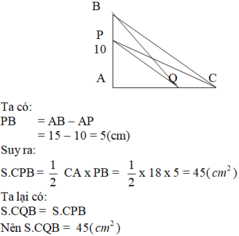
Ta có:

PB = AB – AP

= 15 – 10 = 5(cm)

Suy ra:

S.CPB = 1 2 CA x PB = 1 2 x 18 x 5 = 45( c m 2 )

Nhưng ta lại có:

S.CQB = S.CPB

Nên S.CQB = 45( c m 2 )

1 2 x AB x QC = 45

1 2 x 15 x QC = 45

QC = 6(cm)

Ta suy ra:

AQ = AC – AQ = 18 – 6 = 12(cm)

Do đó ta có

S.APQ = 1 2 AP x AQ = 1 2 x 10 x 12 = 60 ( c m 2 )

Vậy: S.APQ = 60 c m 2

Đúng(0)

AC

Anh Chàng Đào Hoa 6789

4 tháng 7 2016 - olm

Cho tam giác ABC vuông tại A có AB = 9cm, BC =15cm. BI là phân giác góc ABC.

a/ tính ac

b/Kẻ IH vuông góc BC. CM: tam giác AHB cân

#Toán lớp 7

2

CW

Cold Wind

4 tháng 7 2016

Hình đơn giản nên tự vẽ nhá.

a) Áp dụng định lý Py-ta-go vào tam giác vuông ABC:

AC^2 + AB^2 = BC^2
=> AC^2 = BC^2 - AB^2 = 15^2 - 9^2 = 225 - 81 = 144

=> AC = căn 144 = 12 (cm)

b) Xét tam giác BIA và tam giác BIH:

BAI^ = BHI^ = 90o

IBA^ = IBH^

BI chung

=> tam giác BIA = tam giác BIH (cạnh huyền_góc nhọn)

=> BA = BH (2 cạnh tương ứng)

=> Tam giác AHB cân

Đúng(0)

HN

hoàng nam

4 tháng 7 2016

a.Ta có: AB=9cm ; BC=15cm

Theo định lý Py-ta-go: BC²= AB² +AC²

=>AC²=BC² - AB²=15² - 9² = 225-81= 144

AC²= 144 =>AC=\(\sqrt{144}\)=12cm

b.Ta có: IH vuông góc BC tại H => tam giác BIH vuông tại H

Góc A vuông ( tam giác ABC vuông tại A ) => tsm giác ABI vuông tại A

Xét tg BIH và tg ABI có:

góc ABI = góc HBI (BI là phân giác góc B)
BI chung

=> BIH = ABI ( cạnh huyền - góc nhọn)

Do đó: AB = BH

mà đây là 2 cạnh bên của tam giác ABH => ABH cân tại H

Đúng(0)

T

T.Huy

12 tháng 1 2022

Cho tam giác ABC vuông tại A có AH là đường cao. Từ H vẽ HD vuông góc với cạnh AB tại D, vẽ hE vuông góc với cạnh AC tại E. Biết AB = 15cm, BC = 25cm.1)Tính độ dài cạnh AC và diện tích tam giác ABC.2)Chứng minh tứ giác ADHE là hình chữ nhật.3)Trên tia đối của AC lấy điểm F sao cho AF = AE. Chứng minh tứ giác AFDH là hình bình hành.4)Gọi K là điểm đối xứng của B qua A, gọi M là trung điểm của AH. Chứng minh CM vuông góc...

Đọc tiếp

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

12 tháng 1 2022

1: AC=20cm

\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{15\cdot20}{2}=150\left(cm^2\right)\)

2: Xét tứ giác ADHE có

\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)

Do đó: ADHE là hình chữ nhật

3: Xét tứ giác AFDH có

AF//DH

AF=DH

Do đó: AFDH là hình bình hành

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP