Cho hình bình hành ABCD. Gọi E; F và O lần lượt là trung điểm của AB; CD và BD. Gọi I và K là
điểm bất kì trên AD và BC.
a) Chứng minh AI song song CK. b) Chứng minh AE = FC.
c) Chứng minh A; O và C thẳng hàng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 10 2021
Xét tứ giác DEBF có
DE//BF
DE=BF
Do đó: DEBF là hình bình hành
CM
28 tháng 4 2017
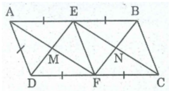
Ta có: Hình chữ nhật EMFN là hình thoi ⇒ ME = MF
ME = 1/2 DE (tính chất hình thoi)
MF = 1/2 AF (tính chất hình thoi)
Suy ra: DE = AF
⇒ Tứ giác AEFD là hình vuông (vì hình thoi có 2 đường chéo bằng nhau)
⇒ ∠ A = 90 0 ⇒ Hình bình hành ABCD là hình chữ nhật.
Ngược lại: ABCD là hình chữ nhật ⇒ ∠ A = 90 0
Hình thoi AEFD có ∠ A = 90 0 nên AEFD là hình vuông
⇒ AF = DE ⇒ ME = MF (tính chất hình vuông)
Hình chữ nhật EMFN là hình vuông (vì có 2 cạnh kề bằng nhau)
Vậy hình chữ nhật EMFN là hình vuông nếu ABCD là hình chữ nhật có AB = 2AD.
AH
Akai Haruma
Giáo viên
9 tháng 11 2021
AEFD và BCFE có phải hình bình hành đâu bạn? Bạn coi lại đề.
5 tháng 11 2021
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
15 tháng 10 2021
a: Xét ΔADE vuông tại E và ΔCBF vuông tại F có
AD=CB
\(\widehat{ADE}=\widehat{CBF}\)
Do đó: ΔADE=ΔCBF
Suy ra: AE=CF
b: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
7 tháng 7 2023
a/
Ta có
AB = CD (cạnh đối hình bình hành)
AE = BE (gt); CF=DF (gt)
=> AE = BE = CF = DF
Xét tứ giác AEFD có
AB//CD (cạnh đối hình bình hành)
=> AE//DF mà AE = DF (cmt) => AEFD là hbh (tứ giác có cặp cạnh đối // và bằng nhau là hình bình hành)
Xét tứ giác AECF có
AB//CD (cạnh đối hbh)
=> AE//CF mà AE = CF => AECF là hình bình hành (lý do như trên)
b/
Do AEFD là hbh => EF=AD (cạnh đối hbh)
C/m tương tự như câu a ta cũng có BEDF là hbh => BF=DE (cạnh đối hbh)
C/m tương tự có AECF là hbh => AF=EC (cạnh đối hbh)
Lời giải:
a. $I\in AD, K\in CB$ mà $AD\parallel CB$ (tính chất hình bình hành)
$\Rightarrow AI\parallel CK$
b.
Do $E$ là trung điểm $AB$ nên $AE=\frac{1}{2}AB$
Do $F$ là trung điểm $CD$ nên $CF=\frac{1}{2}CD$
Mà $AB=CD$ (tính chất hbh)
$\Rightarrow AE=CF$
c.
Tính chất hbh phát biểu rằng 2 đường chéo cắt nhau tại trugn điểm mỗi đường
Do đó $AC$ cắt $BD$ tại trung điểm $BD$. Mà trung điểm của $BD$ là $O$ nên $A,O,C$ thẳng hàng
Hình vẽ:
