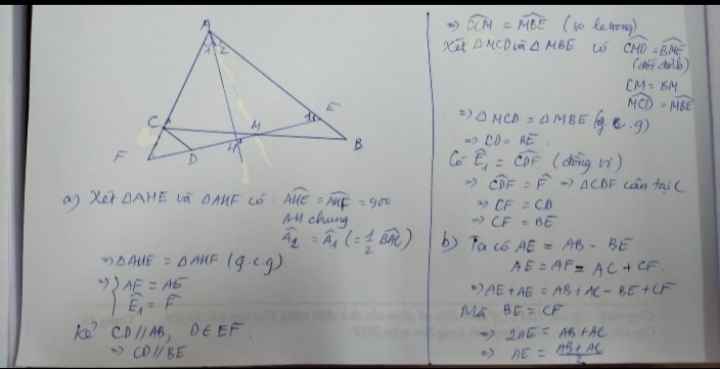
Tam giác ABC có AB >AC. Từ trung điểm M của BC vẽ một đường thẳng vuông góc với tia phân của góc A, cắt tia phân giác tại H, cắt AB,AC lần lượt tại E và F. CMR:
a) BE=CF
b) AE=\(\frac{AB+AC}{2}\) ; BE=\(\frac{AB-AC}{2}\)
c) \(\widehat{BME}=\frac{\widehat{ACB}-\widehat{B}}{2}\)