Cho hình chữ nhật ABCD có độ dài cạnh AB=2a; BC=4a.Tính độ dài vecto AB+vecto AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LN
1
Những câu hỏi liên quan
LN
1
AH
Akai Haruma
Giáo viên
30 tháng 10 2021
Bài này bạn đã đăng tại đây:
https://hoc24.vn/cau-hoi/cho-hinh-chu-nhat-abcd-co-do-dai-canh-ab2a-bc4atinh-do-dai-vecto-abvecto-ac.2659817639735
CM
18 tháng 7 2017
Đọ dài cạnh AD là: 2 x 2 = 4 (cm)
Diện tích hình chữ nhật ABCD là: 4 × 2 = 8 ( c m 3 )
3 tháng 7 2021
Nửa chu vi của hình chữ nhật ABCD (hay Tổng CD và CR) là :
40 : 2 = 20 (cm)
Theo bài ra: Cạnh AB gấp 3 lần BC
=>AB + BC = 3BC + BC = 4BC = 20 cm
=>BC= 5cm
=>AB=5cm* 3=15cm
(bn tự đáp số nha)
Nhớ vote cho mik ^_^
AH
Akai Haruma
Giáo viên
9 tháng 3 2021
Lời giải:
Do $SA\perp (ABCD)$ nên $\angle (SB, ABCD)=\angle (SB, AB)=\widehat{SBA}=45^0$
$\Rightarrow SAB$ là tam giác vuông cân tại $A$
$\Rightarrow SA=AB=a$
Áp dụng định lý Pitago: $SD=\sqrt{SA^2+AD^2}=\sqrt{a^2+(2a)^2}=\sqrt{5}a$
1 tháng 11 2021
\(P_{ABCD}=2\left(AB+AD\right)=2\left(3+3+4\right)=20\left(cm\right)\)
CM
15 tháng 1 2018
Đáp án A
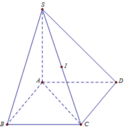
Gọi I là trung điểm của SC. Khi đó I là tâm mặt cầu ngoại
tiếp hình chóp S.ABCD
Ta có: S C = S A 2 + A C 2 = 2 a 2 + 2 a 2 = a 6
Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD là:
R = S C 2 = a 6 2
Lời giải:
Kẻ tia $AL$ đối tia $AB$ sao cho $AB=AL$. Từ $L$ kẻ $LK\perp DC$
\(|\overrightarrow{AB}+\overrightarrow{AC}|=|\overrightarrow{LA}+\overrightarrow{AC}|=|\overrightarrow{LC}|\)
\(=LC=\sqrt{LK^2+KC^2}=\sqrt{BC^2+BL^2}=\sqrt{BC^2+(2AB)^2}=\sqrt{(4a)^2+(2.2a)^2}=4\sqrt{2}a\)