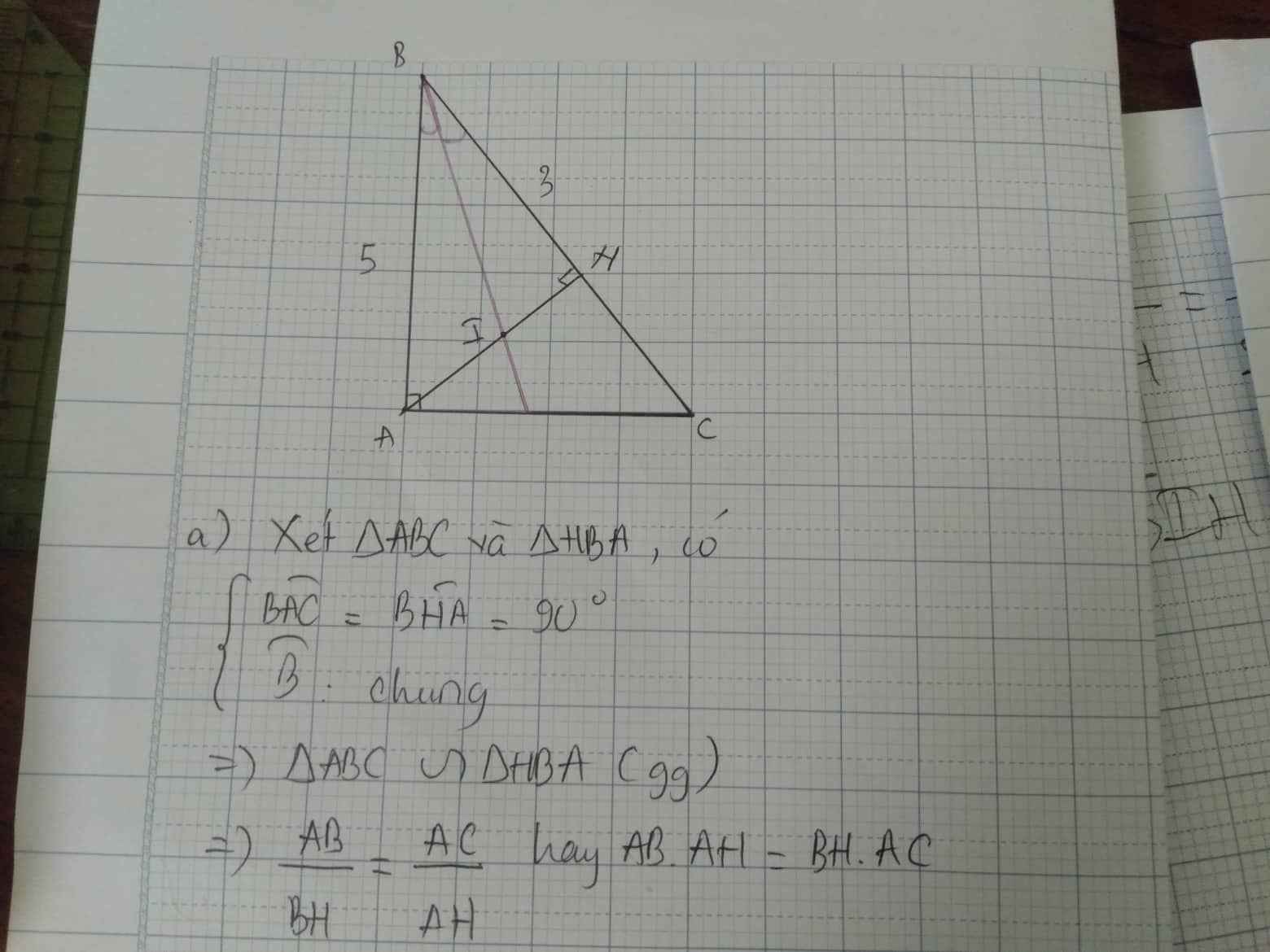
Cho tam giác ABC vuông tại A, đường cao AH
a) CM: tam giác ABC đồng dạng tam giác HBA, từ đó suy ra: AB.AH = BH.AC
b) Tia phân giác góc ABC cắt AC tại I (i). Biết AB=9cm; AC=12cm. Tính AI (ai), BC
c) Tính tỉ số diện tích tam giác HAB và tam giác HCA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 3 2020
tự kẻ hình
a, xét tam giác ABC và tam giác HBA có : góc B chung
góc BAC = góc BHA = 90
=> tam giác ABC đồng dạng với tam giác HBA (g-g)
=> AB/BH = AC/AH
=> AB.AH = BH.AC
b, xét tam giác BAH vuông tại H => HB^2 + HA^2 = AB^2 (Pytago)
BH = 3; AB = 5(gt)
=> 3^2 + AH^2 = 5^2
=> AH^2 = 16
=> AH = 4 do AH > 0
xét tam giác ABH có : BI là pg của góc ABH (gt)
=> AI/AB = IH/BH (tính chất)
=> AI+IH/AB+BH = AI/AB = IH/BH
=> AH/AB + BH = AI/AB = IH/BH
có: AH = 4; AB = 5; BH = 3
=> 4/3+5 = AI/5 = IH/3
=> AI/5 = IH/3 = 1/2
=> AI = 5/2 và IH = 3/2
c, góc CAH = 90 - góc HAB
góc HBA = 90 - góc HAB
=> góc CAH = góc HBA
xét tam giác AHC và tam giác BHA có: góc AHC = góc BHA = 90
=> tam giác AHC đồng dạng với tam giác BHA (g-g)
=> AC/AB = AH/HB
=> AC/AH = AB/HB
BI là pg của tam giác AHB => AI/AH = AB/AB
CK là pg của tam giác AHC => CK/KH = AC/AH
=> AI/AH = CK/KH
=> KI // AC
9 tháng 5 2021
a, Xét △ABC và △HBA có:
∠AHB=∠BAC (=90o), ∠ABC chung
⇒△ABC∼△HBA (g.g)
⇒ \(\dfrac{AB}{BC}=\dfrac{BH}{AB}\) ⇒ AB2=BH.BC
b, Xét △EDC và △BAC có:
∠BAC=∠EDC (=90o) , ∠BCA chung
⇒ △EDC∼△BAC (g.g)
⇒ \(\dfrac{DC}{AC}=\dfrac{EC}{BC}\) ⇒ \(\dfrac{DC}{EC}=\dfrac{AC}{BC}\)
Xét △ADC và △BEC có:
\(\dfrac{DC}{EC}=\dfrac{AC}{BC}\) (C/m trên)
∠BCA chung
⇒ △ADC∼△BEC (c.g.c)
⇒ ∠ADC=∠BEC
9 tháng 5 2021
c, từ b, △ADC∼△BEC
⇒ \(\dfrac{DA}{BE}=\dfrac{AC}{BC}\) (1)
Xét △AHC và △BAC có:
∠AHC=∠BAC (=90o) , ∠BCA chung
⇒ △AHC∼△BAC (g.g)
⇒ \(\dfrac{CH}{AC}=\dfrac{AC}{BC}\) (2)
Từ (1) và (2) ⇒ \(\dfrac{CH}{AC}=\dfrac{DA}{EB}\)
15 tháng 3 2022
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
DO đó: ΔABC\(\sim\)ΔHBA
Suy ra: AB/HB=BC/BA
hay \(AB^2=HB\cdot BC\)
b: \(\widehat{BMH}+\widehat{HBM}=90^0\)
\(\widehat{BNA}+\widehat{ABN}=90^0\)
mà \(\widehat{ABN}=\widehat{HBM}\)
nên \(\widehat{BMH}=\widehat{BNA}\)
26 tháng 2 2022
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
Suy ra: AB/HB=BC/BA
=>BH/AB=BC/BA(1)
hay \(AB^2=BH\cdot BC\)
Câu b đề sai rồi bạn
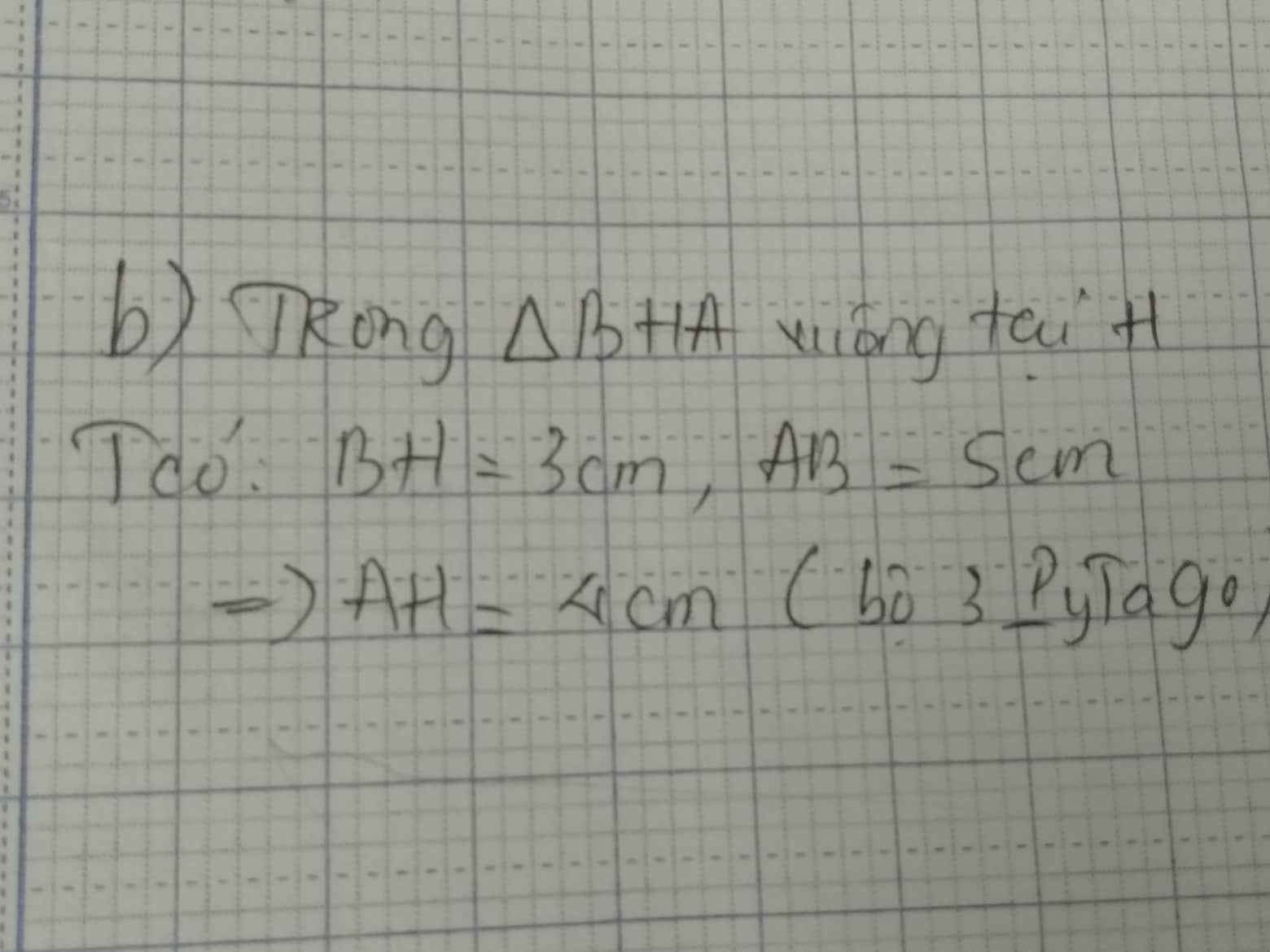
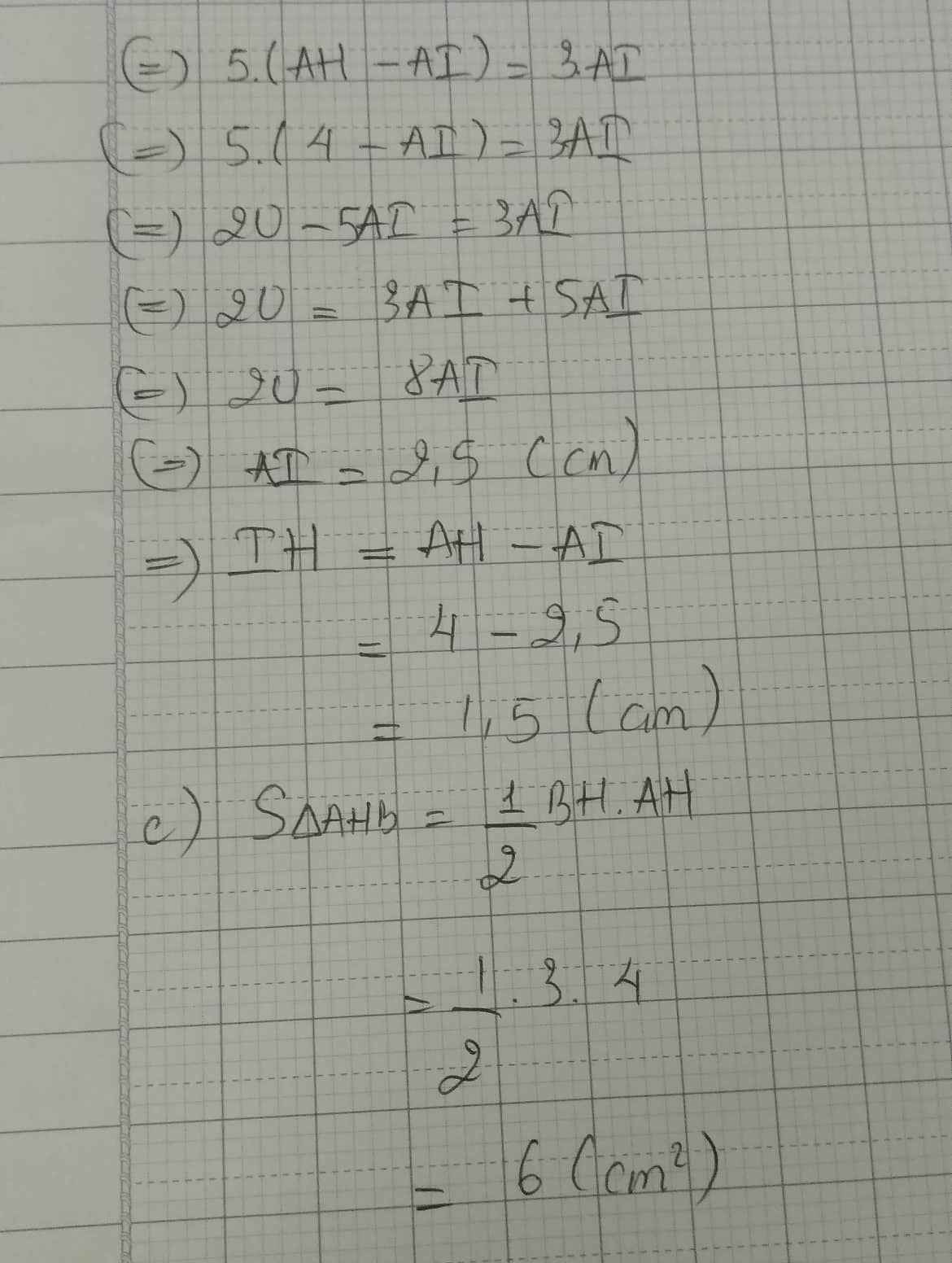
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>AB/HB=AC/HA
=>AB*HA=HB*AC
b: BC=căn 9^2+12^2=15cm
BI là phân giác
=>AI/AB=CI/BC
=>AI/3=CI/5=12/8=1,5
=>AI=4,5cm
c: S HAB/S HCA=(AB/CA)^2