Cho góc xOy bằng 65 độ. Trên tia Ox lấy 2 điểm A và B sao cho A nằm giữa O và B. Trên tia Oy lấy 2 điểm C và D sao cho OA=OC; AB=CD.Tia phân giác của góc xOy cắt AC và DB lần lượt tại M và N
a) C/m tam giác OBD cân
b) tính số đo các góc AMO và BNO
c) C/m AC//BD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

9 tháng 12 2021
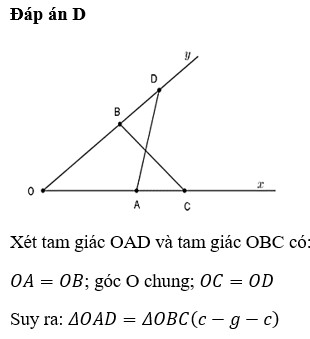
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC

8 tháng 12 2016
Ta có hình vẽ:
a/ Xét tam giác OAD và tam giác OBC có:
OA = OB (GT)
\(\widehat{O}\): góc chung
OC = OD (GT)
Vậy tam giác OAD = tam giác OBC (c.g.c)
b/ Ta có: tam giác OAD = tam giác OBC (câu a)
=> \(\widehat{OAD}\)=\(\widehat{OBC}\) (2 góc tương ứng)
Mà \(\widehat{OAD}\)+\(\widehat{DAC}\) = 1800 (kề bù)
và \(\widehat{OBC}\)+\(\widehat{CBD}\) = 1800 (kề bù)
=> \(\widehat{CAD}\)=\(\widehat{CBD}\)(đpcm)

11 tháng 3 2020
Câu hỏi của nguyenvandat - Toán lớp 7 - Học toán với OnlineMath




a, Ta có: OA + AB = OB
và OC + CD = OD
Mà OA = OC (gt) ; AB = CD (gt)
=> OB = OD
=> △OBD cân tại O
b, Vì ON là tia phân giác của xOy => xON = NOy = xOy : 2 = 65o : 2 = 32,5o
Cách 1: Xét △OAM và △OCM
Có: OA = OC (gt)
AOM = COM (cmt)
OM là cạnh chung
=> △OAM = △OCM (c.g.c)
=> AMO = CMO (2 góc tương ứng)
Mà AMO + CMO = 180o (2 góc kề bù)
=> AMO = CMO = 180o : 2 = 90o
Xét △BON và △DON
Có: OB = OD (cmt)
BON = DON (cmt)
ON là cạnh chung
=> △BON = △DON (c.g.c)
=> BNO = DNO (2 góc tương ứng)
Mà BNO + DNO = 180o (2 góc kề bù)
=> BNO = DNO = 180o : 2 = 90o
Cách 2: Vì OA = OC (gt) => △AOC cân tại O => CAO = (180o - AOC) : 2 = (180o - 65o) : 2 = 115o : 2 = 57,5o
Xét △OAM có: MAO + AMO + MOA = 180o (tổng 3 góc trong tam giác)
=> 57,5o + AMO + 32,5o = 180o
=> AMO = 180o - 32,5o - 57,5o
=> AMO = 90o
Vì △OBD cân tại O => DBO = (180o - BOD) : 2 = (180o - 65o) : 2 = 115o : 2 = 57,5o
Xét △BON có: NBO + BNO + BON = 180o (tổng 3 góc trong tam giác)
=> 57,5o + BNO + 32,5o = 180o
=> BNO = 180o - 32,5o - 57,5o
=> BNO = 90o
c, Vì AMO = 90o => AM ⊥ ON hay AC ⊥ ON (M AC) (1)
AC) (1)
Vì BNO = 90o => BN ⊥ ON hay BD ⊥ ON (N BD) (2)
BD) (2)
=> Từ (1) và (2) => AC // BD (dhnb)