Có bao nhiêu giá trị nguyên trong đoạn - 2018 ; 2018 của tham số m để phương trình 3 x 2 - 3 m x + 1 = 3 3 x 3 + x có 2 nghiệm phân biệt?
A. 4036
B. 4037
C. 2019
D. 2020
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số bậc nhất đồng biến suy ra a > 0 hay m > 2
m thuộc đoạn [-2018; 2018] suy ra m thuộc {3; 4; ...; 2018}
Vậy có 2016 giá trị nguyên của m cần tìm.
Chọn D.

Đáp án A.
Ta có y ' = − 3 x 2 − 6 x + 4 m =>Hàm số nghịch biến trên − ∞ ; 0
⇔ y ' ≤ 0 ∀ x ∈ − ∞ ; 0 ⇔ 4 m ≤ 3 x 2 + 6 x ∀ x ∈ − ∞ ; 0
Bảng biến thiên:
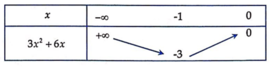
⇒ 3 x 2 + 6 x ≥ − 3 ∀ x ∈ − ∞ ; 0 ⇒ 4 m ≤ 3 x 2 + 6 x ∀ x ∈ − ∞ ; 0
⇔ 4 m ≤ − 3 ⇔ m ≤ − 3 4 ⇒ m ∈ − 2018 ; − 3 4 m ∈ ℤ

Đặt \(g\left(x\right)=-x^4+8x^2+m\Rightarrow g'\left(x\right)=-4x^3+16x\)
\(g'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=0\\x=2\end{matrix}\right.\)
\(f\left(-1\right)=\left|m+7\right|\) ; \(f\left(0\right)=\left|m\right|\) ; \(f\left(2\right)=\left|m+16\right|\) ; \(f\left(3\right)=\left|m-9\right|\)
\(\Rightarrow max\left\{f\left(x\right)\right\}=max\left\{\left|m-9\right|;\left|m+16\right|\right\}\)
TH1: \(\left\{{}\begin{matrix}\left|m+16\right|\ge\left|m-9\right|\\\left|m+16\right|=2018\end{matrix}\right.\) \(\Rightarrow m=2002\)
TH2: \(\left\{{}\begin{matrix}\left|m+16\right|\le\left|m-9\right|\\\left|m-9\right|=2018\end{matrix}\right.\) \(\Rightarrow m=-2027\)
Có 2 giá trị của m

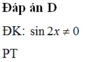
![]()
![]()
![]()
![]()
![]()
![]()
![]()
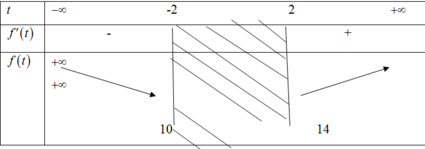
Do đó phương trình có nghiệm khi
![]()
Vậy số giá trị nguyên của α
nhỏ hơn 2018 thỏa mãn yêu cầu
đề bài là ![]()

Đáp án D
Cách giải:
![]()
![]()
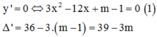
+ ![]() => Hàm số đồng biến trên
=> Hàm số đồng biến trên ![]()
+ ![]() Phương trình (1) có 2 nghiệm phân biệt
Phương trình (1) có 2 nghiệm phân biệt ![]()
Theo đinh lí Viet ta có 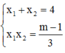
Khi đó, để hàm số đồng biến trên khoảng (1;+∞) thì
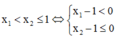
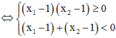
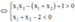
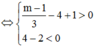 ( vô lí )
( vô lí )
Vậy m ≥ 13
Mà ![]()
![]()
Số giá trị của m thỏa mãn là: 2018 - 13 + 1 = 2006
Chọn đáp án C.
Bình luận:
Quay lại với lời giải ở trên: Ta chia cả 2 vế của (*) cho x chính là chia cả 2 vế của (2) cho