Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A'B' của một vật sáng AB đặt vuông góc với trục chính tại A của một thấu kính hội tụ có tiêu cự f = 20cm và cách thấu kính một khoảng 10cm.
A. ảnh ảo ngược chiều vật
B, ảnh ảo cùng chiều vật
C. ảnh thật cùng chiều vật
D. ảnh thật ngược chiều vật

a)Thấu kính hội tụ cho ảnh A'B' là ảnh thật.
Ảnh A'B' ngược chiều vật và nhỏ hơn vật.
b)Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{30}=\dfrac{1}{45}+\dfrac{1}{d'}\)
\(\Rightarrow d'=90cm\)
Chiều cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{15}{h'}=\dfrac{45}{90}\)
\(\Rightarrow h'=A'B'=30cm\)

a) Ảnh A'B' là ảnh thật, ngược chiều với vật và nhỏ hơn vật.
Tiêu cự của thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{40}+\dfrac{1}{10}=\dfrac{1}{8}\)
\(\Rightarrow f=8cm\)
b)Dịch chuyển vật lại gần thấu kính 10cm thì:
\(d=40-10=30cm\)
Khoảng cách từ ảnh đến vật lúc này:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{8}=\dfrac{1}{30}+\dfrac{1}{d'}\)
\(\Rightarrow d'=\dfrac{120}{11}\approx10,1cm\)
Cần dịch chuyển ảnh một đoạn:
\(\Delta d'=10+10,1=20,1cm\)
Vậy dịch vật ra xa thêm 20,1cm.

Tham khảo:
Ảnh thật, ngược chiều, lớn hơn vật và cách thấu kính một khoảng 60cm.
Lời giải: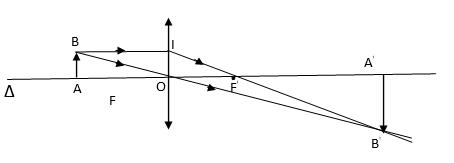
giải tính chiều cao:
ΔOAB ∼ ΔOA'B'
=> \(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\left(1\right)\)
ta lại có :
Δ OIF ∼ Δ A'B'F'
=> \(\dfrac{OI}{A'B'}=\dfrac{OF'}{A'B'}\left(2\right)\)
Từ (1) và (2) suy ra : \(\dfrac{OA}{OA'}=\dfrac{OF'}{A'F'}\left(3\right)\)
mà : A'F' = OA' - OF ' (4)
thay số vào (3) và (4) ta được : OA' = 60cm
Hello mình mới vào nhà bạn