Lời giải:

Ta thấy:

$(-2a^2b^3)^2\geq 0$ với mọi $a,b$

$(3b^2c^4)^5=3^5(b^5c^{10})^2\geq 0$ với mọi $b,c$ 

Do đó để tổng của chúng bằng $0$ thì:

$-2a^2b^3=b^5c^{10}=0$

$\Rightarrow ab=bc=0$

$\Rightarrow$ (a,b,c)=(a,0,c), (0,b,0)$

oki

theo bài ra ta có : a/1=b/4;b/3=c/4 và 4a+b-c=8
+a/1=b/4=>a/3=b/12
+b/3=c/4=>b/12=c/16
=>a/3=b/12=c/16 và 4a+b-c=8
áp dụng tính chất dãy tỉ số = nhau
a/3=b/12=c/16=4a+b-c/4.3+12-16=8/8=1
+a/3=1=>a=3
+b/12=1=>b=12
+c/16=1=>c=16
Vậy a=3;b=12;c=16

(4.3 là 4 nhân ba nha)

đúng thì tick cho mik nha

* bạn ơi, đề bài có phải là x = -6 ko ạ? nếu đúng là nv thì cách giải như thế này nka!

thay x = - 6 vào biểu thức 3x + 5 ta có :

3.(-6) + 5 = -18 + 5 = -13 

=4/(2x)²-9+5

=4/4x²-4

đến đây b tự lm nha

Gọi số học sinh của lớp 7A,7B,7C lần lượt là a,b,c ( \(a,b,c\in\) N^* )

Theo đề bài ta có :

a,b,c tỉ lệ với 3,5,7 

= > \(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}\) và a + b + c = 105

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c}{3+5+7}=\dfrac{105}{15}=7\)

\(\dfrac{a}{3}=7=>a=21\)

\(\dfrac{b}{5}=7=>b=35\)

\(\dfrac{c}{7}=7=>c=49\)

Vậy số học sinh của các lớp 7A,7B, 7C lần lượt là 21 , 35 , 49 

a, Xét tam giác \(\Delta ABH\) và \(\Delta ACH\) có :

\(HB=HC\left(gt\right)\)

\(\widehat{B}=\widehat{C}\left(gt\right)\)

\(AB=AC\left(gt\right)\)

= > \(\Delta ABH=\Delta ACH\left(c-g-c\right)\)

b, M là trung điểm của cạnh AC = > MA = 1/2 AC ( 1 )

 N là trung điểm của cạnh AB = > NA = 1/2 AB  ( 2 )

Từ ( 1 ) , ( 2 ) = > MA = NA   ( Do AB = AC )

Mà tam giác ABH = tam giác ACH ( câu a, )

= > \(\widehat{BAH}=\widehat{CAH}\) ( 2 góc tương ứng )

Xét \(\Delta ANH\) và \(\Delta AMH\) có :

\(AN=AM\left(cmt\right)\)

\(\widehat{BAH}=\widehat{CAH}\left(cmt\right)\)

AH chung 

= > \(\Delta ANH=\Delta AMH\left(c-g-c\right)\)

= > HN = HM ( 2 cạnh tương ứng )

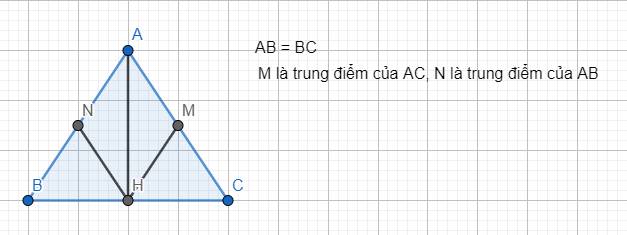
a) Xét hai tam giác ABH và ACH ta có:

- AB = AC (vì ABC là tam giác cân)

- HB = HC (vì H là trung điểm của BC)

- \(\widehat{B}=\widehat{C}\) (vì ABC là tam giác cân)

Vậy \(\Delta ABH=\Delta ACH\) (c.g.c)

b) Xét hai tam giác NBH và MCH ta có:

- NB = MC (vì AB = AC, M là trung điểm của AC và N là trung điểm của AB)

- HB = HC (đã chứng minh trên)

- \(\widehat{B}=\widehat{C}\) (đã chứng minh trên)

Suy ra \(\Delta NBH=\Delta MCH\) (c.g.c)

Khi đó HN = HM (vì hai cạnh tương ứng)