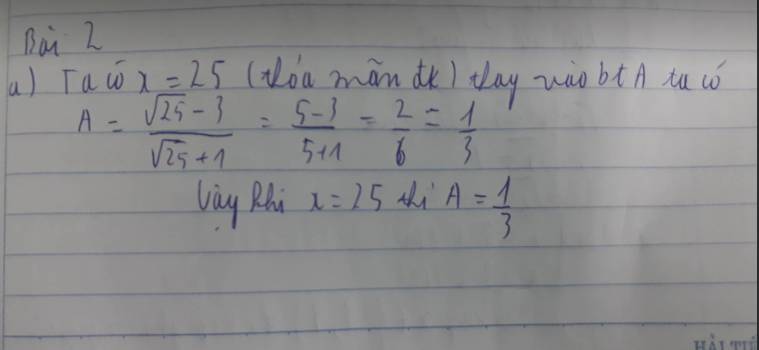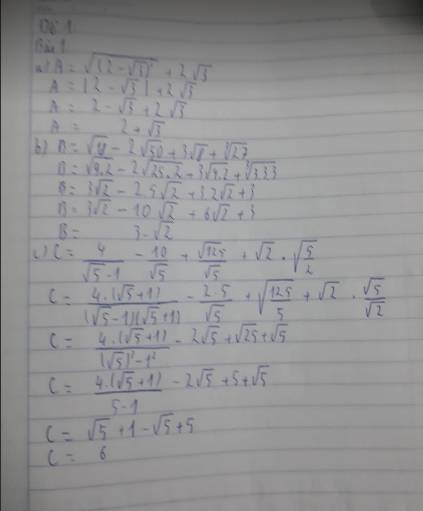(4 điểm) Cho tam giác $A B C$ vuông tại $A$, đường cao $A H(H \in B C)$.
a) Biết $A B=12 \mathrm{~cm}, B C=20 \mathrm{~cm}$, Tính $A C, A H$ và $\widehat{A B C}$ ( làm tròn đến độ);
b) Kẻ $H M$ vuông góc với $A B$ tại $M, H N$ vuông góc với $A C$ tại $N$. Chứng minh: $A N . A C=A C^2-H C^2$
c) Chứng minh: $A H=M N$ và $A M \cdot M B+A N \cdot N C=A H^2$;
d) Chứng minh: $\tan ^3 C=\dfrac{B M}{C N}$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Đk: \(x+5\ge0\Rightarrow x\ge-5\)
\(\sqrt{4x+20}-2\sqrt{x+5}+\sqrt{9x+45}=12\\ \Leftrightarrow\sqrt{4\left(x+5\right)}-2\sqrt{x+5}+\sqrt{9\left(x+5\right)}=12\\ \Leftrightarrow2\sqrt{x+5}-2\sqrt{x+5}+3\sqrt{x+5}=12\\ \Leftrightarrow3\sqrt{x+5}=12\\ \Leftrightarrow\sqrt{x+5}=4\\ \Leftrightarrow x+5=16\\ \Rightarrow x=11\)
b.
\(\sqrt{x^2-10x+25}=6\)
Đk: \(x^2-10x+25=\left(x-5\right)^2\ge0;\forall x\inℝ\)
\(\sqrt{x^2-10x+25}=6\\ \Leftrightarrow\sqrt{\left(x-5\right)^2}=6\\ \Rightarrow|x-5|=6\)
\(\Rightarrow\left[{}\begin{matrix}x-5=6\\x-5=-6\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=11\\x=-1\end{matrix}\right.\)
Đs....

a) A=√(2-√3)2 + 2√3
= |2-√3| + 2√3
= 2 - √3 + 2√3
= 2 + √3
b) B = √18 - 2√50 +3√8 + ∛27
= 3√2 - 10√2 + 6√2 + 3
= 3 - √2
c) C = { 4 / ( √5 - 1 ) } - ( 10 / √5 ) + ( √125 / √5) + √2 ✖ √5/2
= 4(√5 + 1) / 4 - 2√5 + 5 + √5
= 2√5 + 2 - 2√5 + 5 + √5
= 7 + √5


Sửa lại đề là tìm tất cả các số nguyên a nhé.
Ta có \(A=a^4+a^3+a^2=a^2\left(a^2+a+1\right)\)
Để ý rằng nếu \(a>0\) thì \(a^2+a+1>a^2\) và \(a^2+a+1< a^2+2a+1=\left(a+1\right)^2\) , hay \(a^2< a^2+a+1< \left(a+1\right)^2\). Dẫn đến \(a^2+a+1\) không là SCP và đương nhiên \(A=a^2\left(a^2+a+1\right)\) không là số chính phương.
Nếu \(a< -1\) thì \(a^2+a+1>a^2+2a+1=\left(a+1\right)^2\) và \(a^2+a+1< a^2\). Từ đó \(\left(a+1\right)^2< a^2+a+1< a^2\) hay \(a^2+a+1\) không phải là SCP, do đó \(A=a^2\left(a^2+a+1\right)\) không là số chính phương.
Do vậy \(-1\le a\le0\) hay \(a\in\left\{-1;0\right\}\). Thử lại, ta thấy cả 2 số này thỏa mãn.
Vậy để A có giá trị là số chính phương thì \(a\in\left\{-1;0\right\}\)

Ta có \(M=\dfrac{sin48^{\text{o}}}{cos42^{\text{o}}}-cos60^{\text{o}}+tan27^{\text{o}}.tan63^{\text{o}}\)
\(=\dfrac{sin48^{\text{o}}}{sin48^o}-cos60^{\text{o}}+tan27^o.cot27^o=1-cos60^{\text{o}}+1\)
\(=2-cos60^{\text{o}}=2-\dfrac{1}{2}=\dfrac{3}{2}\)
N = \(cot27^{\text{o}}.cot60^{\text{o}}.cot63^{\text{o}}+sin^244^{\text{o}}+sin^246^{\text{o}}\)
\(=cot27^{\text{o}}.tan27^{\text{o}}.cot60^{\text{o}}+sin^244^{\text{o}}+cos^244^{\text{o}}=cot60^{\text{o}}+1=\dfrac{1}{\sqrt{3}}+1\)
\(=\dfrac{\sqrt{3}+3}{3}\)