\(\dfrac{5}{7}< \dfrac{14}{?}< \dfrac{5}{6}\)

\(\dfrac{5x14}{7x14}< \dfrac{14x5}{?x5}< \dfrac{5x14}{6x14}\)

\(\dfrac{70}{98}< \dfrac{70}{?x5}< \dfrac{70}{84}\)

98>?x5 >84

? = 17 hoặc 18

\(\dfrac{5}{7}\) < \(\dfrac{14}{?}\) < \(\dfrac{5}{6}\)

Gọi số cần điền vào chỗ ? là \(x\) và \(x\) là số tự nhiên khác 0 thì ta có:

\(\dfrac{5}{7}\) < \(\dfrac{14}{x}\) < \(\dfrac{5}{6}\) 

\(\dfrac{5\times14}{7\times14}\) < \(\dfrac{14\times5}{x\times5}\) < \(\dfrac{5\times14}{6\times14}\)

\(\dfrac{70}{98}\) < \(\dfrac{70}{x\times5}\) < \(\dfrac{70}{84}\)

98 > \(x\times5\) > 84( vì các phân số có cùng tử số phân số nào có mẫu lớn hơn thì phân số đó nhỏ hơn)

98: 5 > \(x\) > 84 : 5 ⇒19,6 > \(x\) >16,8

Vì \(x\) là số tự nhiên nên \(x\)  = 19; 18; 17

Vậy số thích hợp điền vào chỗ ? là 17; 18; 19

Đáp số: 17; 18; 19

Gọi số cần tìm là ab6

Theo bài ra ta có:

ab6 - ab = 807

ab x 10 + 6 - ab = 807

6 + ab x 10 - ab = 807

6 + ab x 9          = 807

ab x 9 + 6         = 807

ab x 9               = 807 - 6

ab x 9               = 801

ab                     = 801 : 9

ab                     = 89

=> Số cần tìm là :896

Khi bỏ đi chữ số 6 ở tận cùng thì ta được số mới nên số cũ gấp 10 lần số mới và 6 đơn vị

Theo bài ra ta có sơ đồ:

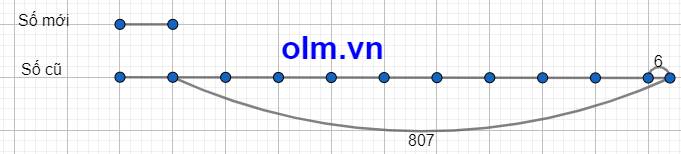
Theo sơ đồ ta có: Số mới là: (807 - 6): (10-1) = 89

Số cũ cần tìm là: 89 \(\times\) 10 + 6 = 896

Đáp số: 896

Khi xe taxi khởi hành thì xe khách cách xe taxi là:

42 \(\times\) 1 = 42(km)

Thời gian hai xe gặp nhau là:

42: ( 63 - 42) = 2 (giờ)

Vị trí gặp nhau cách B là:

152 - 63 \(\times\) 2 = 26 (km)

Đáp số: 26 km 

Khi xe taxi khởi hành thì xe khách cách xe taxi là:

42 $\times$ 1 = 42(km)

Thời gian hai xe gặp nhau là:

42: ( 63 - 42) = 2 (giờ)

Vị trí gặp nhau cách B là:

152 - 63 $\times$ 2 = 26 (km)

Đáp số: 26 km 

A = 47 + 47 + 47+.....+ 47 + 33 + 33 + ....+ 33

A = (47 + 47 + 47 + ...+ 47) + ( 33 + 33 +....+33)

A = (47 \(\times\) 1 + 47 \(\times\) 1 + ....+47 \(\times\)1) + ( 33 \(\times\) 1 + 33 \(\times\) 1+...+ 33 \(\times\) 1)

A = 47 \(\times\) ( 1 + 1+...+1) + 33 \(\times\)( 1 + 1 +....+1)

A = 47 \(\times\) 67 + 33 \(\times\) 47

A = 47 \(\times\)( 67 + 33)

A = 47 \(\times\)100

A = 4700

47 + 47 + ...+ 47 + 33 + 33 + ... + 33

= 47 x 67 + 33 x 47

=3149+1551

=4700

B = \(\dfrac{8}{3}\): \(\dfrac{1}{3\%}\) + 0,14

B = \(\dfrac{8}{3}\) \(\times\) \(\dfrac{3\%}{1}\) + 0,14

B = \(\dfrac{8}{3}\) \(\times\) \(\dfrac{3}{100}\) + 0,14

B = 0,08 + 0,14

B = 0,22

\(\dfrac{3}{1\times4}+\dfrac{3}{4\times7}+...+\dfrac{3}{226\times229}\)

\(=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+....+\dfrac{1}{226}-\dfrac{1}{229}\)

\(=1+\left(-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+....+\dfrac{1}{226}\right)-\dfrac{1}{229}\)

\(=1+0-\dfrac{1}{229}\)

\(=1-\dfrac{1}{229}\)

\(=\dfrac{229}{229}-\dfrac{1}{229}\)

\(=\dfrac{229-1}{229}\)

\(=\dfrac{228}{229}\)

Đây là dạng tính nhanh tổng phân số mà tử số bằng hiệu hai thừa số dưới mẫu.

Kiến thức cần nhớ: 

+ Tử số bằng hiệu hai thừa số dưới mẫu. Mẫu thứ nhất của phân số này là mẫu thứ hai của phân số kia.

+ Tách từng phân số thành hiệu hai phân số

+ Triệt tiêu các phân số giống nhau

+ Thu gọn ta được tổng cần tính

A = \(\dfrac{3}{1\times4}\) + \(\dfrac{3}{4\times7}\)+...+ \(\dfrac{3}{226\times229}\)

A = \(\dfrac{1}{1}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{7}\) + ...+ \(\dfrac{1}{226}\) - \(\dfrac{1}{229}\)

A = 1 - \(\dfrac{1}{229}\)

A = \(\dfrac{228}{229}\)

    A = 1³ + 2³ + 3³ + 4³ +...+ 100³

   Ta có:   B = 1³ + 2³ + 3³ + 4³ +...+ n³ = ( 1 + 2 + 3 +...+n)²

   Thật vậy Với n = 1 ta có: B = 1³ = 1² (đúng)

 Giả sử B đúng với n = k tức là:1³ + 2³ + 3³ +....+k³ = (1+2+3 +...+k)²

Ta cần chứng minh B  đúng với n = k + 1. 

⇔1³ + 2³ + 3³ + ...+ k³ + (k+1)³ = (1+2+3+...+k+k+1)² 

Ta có:

B = 1³ + 2³ + 3³ +....+ k³ + (k+1)³

B = (1+2+3+...+k)² + (k + 1)³

B = {(k +1)k:2}² + (k+1)³ = (k+1)²{ \(\dfrac{k^2}{4}\) + k + 1} =(k+1)²(k²+4k+4)²: 4

B = (k+1)²(k²+2k + 2k + 4): 4 = (k+1)²{(k(k+2) + 2(k+2)}: 4

B = (k+1)²(k+2)²:4 = {(k+1)(k+2): 2}²

Mặt khác 1 + 2 + 3 + 4 +....+ k + k + 1 = (k+2)(k+1): 2

⇒B = (1+2+3+...+ k+1)² (đpcm)

Vậy 1³ + 2³ + 3³ + ...+n³ = (1+2+3+...+n)² 

Áp dụng công thức trên ta có:

A = 1³ + 2³ + 3³ +4³ +...+100³ = (1+2+3+4...+100)²

C = 1 + 2 + 3 + 4 +...+100

Dãy số trên là dãy số cách đều với khoảng cách là 2 - 1 = 1

Số số hạng của dãy số trên là: (100 -1):1 + 1 = 100

Tổng dãy số trên là: C = (100 +1)\(\times\) 100  : 2 = 5050

A = 5050²

  A = 13 + 23 + 33 + 43 +...+ 1003

   Ta có:   B = 13 + 23 + 33 + 43 +...+ n3 = ( 1 + 2 + 3 +...+n)2

   Thật vậy Với n = 1 ta có: B = 13 = 12 (đúng)

 Giả sử B đúng với n = k tức là:13 + 23 + 33 +....+k3 = (1+2+3 +...+k)2

Ta cần chứng minh B  đúng với n = k + 1. 

⇔13 + 23 + 33 + ...+ k3 + (k+1)3 = (1+2+3+...+k+k+1)2 

Ta có:

B = 13 + 23 + 33 +....+ k3 + (k+1)3

B = (1+2+3+...+k)2 + (k + 1)3

B = {(k +1)k:2}2 + (k+1)3 = (k+1)2{ $\genfrac{}{}{0ex}{}{k^2}{4}$ + k + 1} =(k+1)2(k2+4k+4)2: 4

B = (k+1)2(k2+2k + 2k + 4): 4 = (k+1)2{(k(k+2) + 2(k+2)}: 4

B = (k+1)2(k+2)2:4 = {(k+1)(k+2): 2}2

Mặt khác 1 + 2 + 3 + 4 +....+ k + k + 1 = (k+2)(k+1): 2

⇒B = (1+2+3+...+ k+1)2 (đpcm)

Vậy 13 + 23 + 33 + ...+n3 = (1+2+3+...+n)2 

Áp dụng công thức trên ta có:

A = 13 + 23 + 33 +43 +...+1003 = (1+2+3+4...+100)2

C = 1 + 2 + 3 + 4 +...+100

Dãy số trên là dãy số cách đều với khoảng cách là 2 - 1 = 1

Số số hạng của dãy số trên là: (100 -1):1 + 1 = 100

Tổng dãy số trên là: C = (100 +1)$\times$ 100  : 2 = 5050

A = 50502

HT!

Trả lời đi

Bài 8:

Chiều dài ban đầu của thửa ruộng hình chữ nhật là:

500 : 5 = 100 (m)

Chiều rộng ban đầu của thửa ruộng hình chữ nhật là:

375 : 100 = 3,75 (m)

Chu vi của thửa ruộng ban đầu là:

(100 + 3,75) \(\times\) 2 = 207,5 (m)

Đáp số: 207,5 m

Trường hợp xấu nhất sẽ bốc phải:

12 bi màu tím + 10 viên bi đỏ = 22 ( viên bi)

Dể chắc chắn có đủ cả 3 màu bi thì cần bốc ít nhất số bi là:

22 + 1 = 23 ( viên bi)

Đáp số: 23 viên bi.

Số viên Sơn phải lấy để có đủ cả 4 màu bi là:

8 + 10 + 4 = 22 ( viên bi )

Đáp số : 22 viên bi

Uả rồi đề kiểu thế thì ai làm đc hả bà?