a) Ta có \(0,625^{200}=\left(\dfrac{5}{8}\right)^{200}\) và \(0,5^{1000}=\left(\dfrac{1}{2}\right)^{1000}=\left(\dfrac{1}{2}\right)^{5.200}\) \(=\left[\left(\dfrac{1}{2}\right)^5\right]^{200}\) \(=\left(\dfrac{1}{32}\right)^{200}\). Mà hiển nhiên \(\left(\dfrac{5}{8}\right)^{200}>\left(\dfrac{1}{32}\right)^{200}\) nên suy ra \(0,625^{200}>0,5^{1000}\)

b) Ta thấy \(\left(-32\right)^{27}< 0\) trong khi \(\left(-27\right)^{32}>0\) nên đương nhiên \(\left(-32\right)^{27}< \left(-27\right)^{32}\)

c) Ta thấy \(-\dfrac{3}{2}>-2\) nên \(\left(-\dfrac{3}{2}\right)^5>\left(-2\right)^5\)

                                           bài giải

1 người làm trong số ngày là :

11 x 63 = 693 ( ngày )

Số người sau khi bổ sung là :

693 : 7 = 99 ( người )

Số người muốn làm xong quãng đường đó trong 7 ngày là :

99 - 63 = 36 ( người )

Đáp số : 36 người

a)Sau 1 năm bác 5 rút được 500000000đ

 b) Sang năm thứ 2,vốn là 275000000đ bác lãi tổng là 5,5%

`a)` \(18\le2x\le150\\ =>\dfrac{18}{2}\le x\le\dfrac{150}{2}\\ =>9\le x\le75\)

\(A=\left\{9;10;11;12;...;75\right\}\)

`b)` Số phần tử tập hợp A :

   \(\left(75-9\right):1+1=67\) (phần tử)

Tổng tập hợp A :

    \(\left(75+9\right).67:2=2814\)

$a)$ $18\le 2x\le 150=>\genfrac{}{}{0ex}{}{18}{2}\le x\le \genfrac{}{}{0ex}{}{150}{2}=>9\le x\le 75$

$A=\left\{9;10;11;12;...;75\right\}$

$b)$ Số phần tử tập hợp A :

   $\left(75-9\right):1+1=67$ (phần tử)

Tổng tập hợp A :

    $\left(75+9\right).67:2=2814$

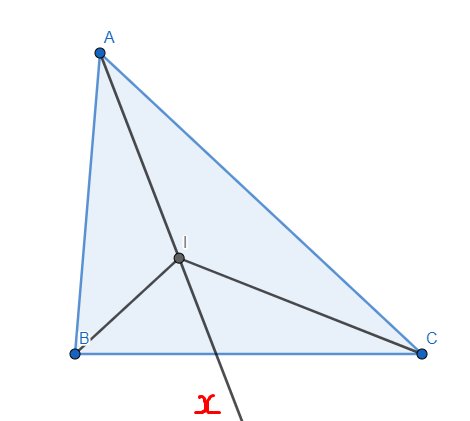
 Kẻ tia phân giác Ax của tam giác ABC. Theo tính chất góc ngoài của tam giác, dễ có \(\widehat{BIx}=\widehat{IBA}+\widehat{IAB}\) và \(\widehat{CIx}=\widehat{ICA}+\widehat{IAC}\). Cộng theo vế 2 đẳng thức trên, thu được \(\widehat{BIC}=\dfrac{\widehat{ABC}}{2}+\dfrac{\widehat{ACB}}{2}+\widehat{ABC}\) \(=\dfrac{180^o+\widehat{ABC}}{2}\) \(=90^o+\dfrac{\widehat{BAC}}{2}\)

 Tới đây mình cũng đã chứng minh xong câu b luôn rồi. Bạn chỉ cần thay số đo góc vào thì tính được câu a.

a) (BI và CI lần lượt là các đường phân giác của góc B và C)

Theo đề ta có:

\(\widehat{IBC}+\widehat{ICB}+\widehat{BIC}=180^o\)

\(\Leftrightarrow\widehat{IBC}+\widehat{ICB}=180^o-\widehat{BIC}=180^o-140^o=40^o\)

Mà \(\widehat{ABI}=\widehat{CBI}\) và \(\widehat{ACI}=\widehat{BCI}\) (vì BI và CI lần lượt là các đường phân giác của góc B và C)

Suy ra \(\widehat{ABC}+\widehat{ACB}=2\widehat{IBC}+2\widehat{ICB}=2\left(\widehat{IBC}+\widehat{ICB}\right)=2\cdot40^o=80^o\)

Từ đó 

\(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^o\)

\(\Leftrightarrow\widehat{BAC}=180^o-\left(\widehat{ABC}+\widehat{ACB}\right)=180^o-80^o=100^o\)

\(\left(-\dfrac{1}{2}\right)-\left(-\dfrac{3}{5}\right)+\left(-\dfrac{1}{9}\right)+\dfrac{1}{127}-\dfrac{7}{18}+\dfrac{4}{35}-\left(-\dfrac{2}{7}\right)\)

\(=\left[-\dfrac{1}{2}-\dfrac{1}{9}-\dfrac{7}{18}\right]+\left[\dfrac{3}{5}+\dfrac{4}{35}+\dfrac{2}{7}\right]+\dfrac{1}{127}\)

\(=-\dfrac{18}{18}+\dfrac{35}{35}+\dfrac{1}{127}\)

\(=-1+1+\dfrac{1}{127}\)

\(=\dfrac{1}{127}\)

`@` `\text {Ans}`

`\downarrow`

\((x+ 3y)(x - 2у)\)

`= x(x-2y) + 3y(x-2y)`

`= x^2 - 2xy + 3xy - 6y^2`

`= x^2 + xy - 6y^2`

   6a - [ b + 3a - (4a - b)]

= 6a - [ b + 3a - 4a + b]

= 6a - [2b - a]

= 6a - 2b + a

= 7a - 2b

A>B

a>b

YC ĐỀ LÀ GÌ EM?

tính