cho tam giác ABC cs 3 góc nhọn các đường cao AD BE CF cắt nhau tại H
a) Cm Tg AEHF- BDHF -CDHE -ABDE- ACDF BCEF (ko lm cx đc)
b)gọi I là trung điểm của AH,O là trung điểm BC. Cm OE là tiếp tuyến của đtr (i) dk AH, IE là tiếp tuyến của đtr(o) dk BC
C)Cm H là tâm đtr nt tam giác DEF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\begin{equation}
\begin{aligned}
& (a c+b d)^2+(a d-b c)^2 \\
& =a^2 c^2+2 a b c d+b^2 d^2+a^2 d^2-2 a b c d+b^2 c^2 \\
& =\left(a^2 c^2+a^2 d^2\right)+\left(b^2 d^2+b^2 c^2\right) \\
& =a^2\left(c^2+d^2\right)+b^2\left(d^2+c^2\right) \\
& =\left(c^2+d^2\right)\left(a^2+b^2\right)
\end{aligned}
\end{equation}
với a,b >0 CMR (\(\sqrt{a}\)+\(\sqrt{b}\))(\(\dfrac{1}{\sqrt{a+3b}}\)+\(\dfrac{1}{\sqrt{3b+a}}\)) ≤2

Chắc đề ghi nhầm ngoặc sau (2 mẫu kia thực chất giống nhau, lẽ ra phải là \(\dfrac{1}{\sqrt{a+3b}}+\dfrac{1}{\sqrt{3a+b}}\)
\(VT=\sqrt{\dfrac{a}{a+3b}}+\sqrt{\dfrac{a}{3a+b}}+\sqrt{\dfrac{b}{a+3b}}+\sqrt{\dfrac{b}{3a+b}}\)
\(=\sqrt{\dfrac{a}{a+b}.\dfrac{a+b}{a+3b}}+\sqrt{\dfrac{1}{2}.\dfrac{2a}{3a+b}}+\sqrt{\dfrac{1}{2}.\dfrac{2b}{a+3b}}+\sqrt{\dfrac{b}{a+b}.\dfrac{a+b}{3a+b}}\)
\(\le\dfrac{1}{2}\left(\dfrac{a}{a+b}+\dfrac{a+b}{a+3b}\right)+\dfrac{1}{2}\left(\dfrac{1}{2}+\dfrac{2a}{3a+b}\right)+\dfrac{1}{2}\left(\dfrac{1}{2}+\dfrac{2b}{a+3b}\right)+\dfrac{1}{2}\left(\dfrac{b}{a+b}+\dfrac{a+b}{3a+b}\right)\)
\(=\dfrac{1}{2}\left(1+\dfrac{a+b}{a+b}+\dfrac{a+3b}{a+3b}+\dfrac{3a+b}{3a+b}\right)=2\)
Dấu "=" xảy ra khi \(a=b\)

Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn.
Viết đề như thế này rất khó đọc.

\(M=\dfrac{\sqrt{a\left(a+2b\right)}+\sqrt{b\left(b+2a\right)}}{a+b}\le\dfrac{\sqrt{\left(a+b\right)\left(a+2b+b+2a\right)}}{a+b}=\sqrt{3}\)
Vậy \(M_{max}=\sqrt{3}\) khi \(a=b\)
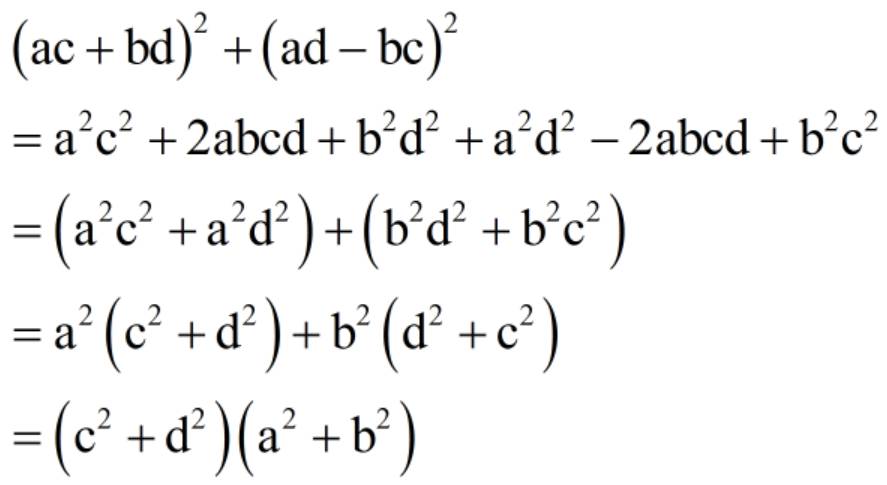
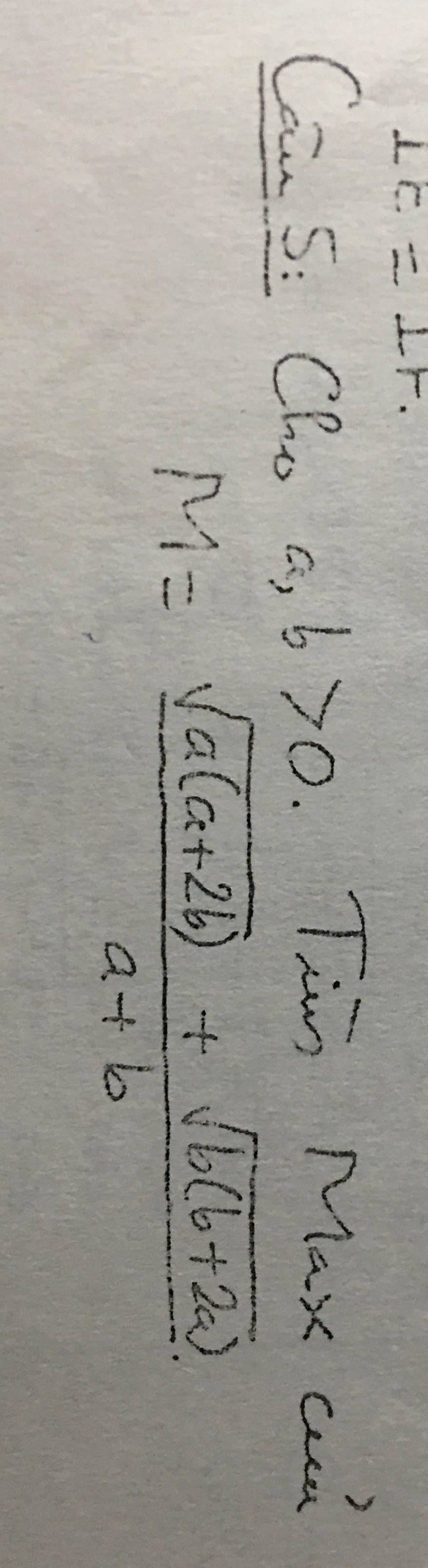
help me