52 x 100 x 4 

= 5200 x 4 

= 20800

52 x 100 x 4

= 5200 x 4

= 20800

dễ

2,7 kg nhé

3002 \(\times\) 0,58 - 0,58 - 0,58 \(\times\) 2001

= 3002 \(\times\) 0,58 - 0,58 \(\times\) 1 - 0,58 \(\times\) 2001

= 0,58 \(\times\) ( 3002 - 1 - 2001)

= 0,58 \(\times\) 1000

= 580

300 \(\times\) 0,08 + 0,08 \(\times\) 699 + 0,08

= 300 \(\times\) 0,08 + 0,08 \(\times\) 699 + 0,08 \(\times\) 1

= 0,08 \(\times\) ( 300 + 699 + 1)

= 0,08 \(\times\) 1000

= 80

49,50,51 nhé

Trung bình cộng của ba số tự nhiên liên tiếp bằng số thứ hai

Số thứ hai là: 150 : 3 = 50

Số thứ nhất là: 50 - 1 = 49

Số thứ ba là: 50 + 1 = 51

Đáp số: 49; 50; 51

\(\dfrac{13+x}{20}=\dfrac{15}{20}\)

\(13+x=15\)

\(x=2\)

Bạn xem lại xem đã viết đề đúng chưa vậy?

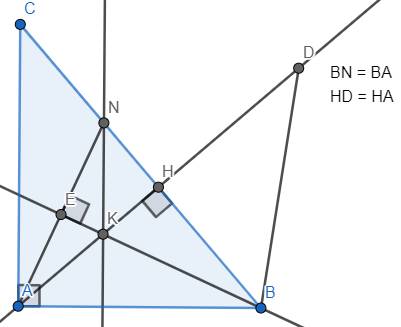
a) Xét ΔABE vuông tại E & ΔNBE vuông tại E có:

- BE là cạnh chung, BN = BA (giả thuyết)

Suy ra ΔABE = ΔNBE (cạnh huyền - cạnh góc vuông)

b) Theo đề ta có BH vuông góc với AD và HA = HD

Suy ra BH là đường trung trực của AD

Suy ra BA = BD (vì B nằm trên đường trung trực của AD)

c) Trong ΔNAB có AH và BE là đường cao, đồng quy tại điểm K

Suy ra NK là đường cao của ΔNAB, hay NK vuông góc với AB

Mà AC cũng vuông góc với AB, suy ra NK // CA

a. - Vì BE vuông góc với AN (gt)
=> tam giác ABE vuông tại E (tc)
     tam giác NBE vuông tại E (tc)
- Xét tam giác vuông ABE và tam giác vuông NBE, có:
    + Chung BE
    + BA = BN (gt)
=> tam giác vuông ABE = tam giác vuông NBE (Cạnh huyền - cạnh  góc vuông)

b. - Vì AH là đường cao của tam giác ABC (gt)
=> tam giác ABH vuông tại H
     tam giác DBH vuông tại H
- Xét tam giác vuông ABH và tam giác vuông DBH, có:
    + Chung BH
    + HA = HD (gt)
=> tam giác vuông ABH = tam giác vuông DBH (2 cạnh góc vuông)
    => BA = BD (2 cạnh tương ứng)