Cho đường tròn tâm O đường kính AB, lấy điểm C thuộc đường tròn tâm O, với điểm C không trùng A và B. Gọi I là trung điểm của dây AC, D là giao điểm của tia OI và tiếp tuyến của đường tròn tâm O tại A. a) Chứng minh tam giác ABC vuông. b) Chứng minh DC là tiếp tuyến của đường tròn tâm O. Chứng minh DC2=DI.DO c) Tia phân giác của góc BAC cắt dây BC tại điểm E và cắt đường tròn tâm O tại F, với F không trùng với A. Chứng minh rằng FA.FE=FB2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/
Ta có A và E cùng nhìn BC dưới 1 góc vuông => ACBE là tứ giác nội tiếp đường tròn đường kính BC
\(\Rightarrow\widehat{AEC}=\widehat{ABC}\) (góc nội tiếp cùng chắn cung AC) (1)
Xét tg vuông ABC có \(\widehat{ABC}+\widehat{ACB}=90^o\)
Xét tg vuông ACD có \(\widehat{CAD}+\widehat{ACB}=90^o\)
\(\Rightarrow\widehat{ABC}=\widehat{CAD}\) (cùng phụ với \(\widehat{ACB}\)) (2)
Từ (1) và (2) \(\Rightarrow\widehat{AEC}=\widehat{CAD}\)
Xét \(\Delta CAI\) và \(\Delta CEA\) có
\(\widehat{AEC}=\widehat{CAD};\widehat{ACE}\) chung \(\Rightarrow\Delta CAI\) đồng dạng với \(\Delta CAE\) (g.g.g)
b/

\(2xy-3y+3x=7\)
\(\Leftrightarrow4xy-6y +6x=14\)
\(\Leftrightarrow2y\left(2x-3\right)+6x-9=5\)
\(\Leftrightarrow2y\left(2x-3\right)+3\left(2x-3\right)=5\)
\(\Leftrightarrow\left(2x-3\right)\left(2y+3\right)=5\)
Vì \(x,y\in N\)\(\Rightarrow2y+3\ge3\)\(\Rightarrow2y+3\inƯ\left(5\right)=\left\{5\right\}\)
\(\Rightarrow2y+3=5\Leftrightarrow y=1\)
\(\Rightarrow\left(2x-3\right)\left(2+3\right)=5\)
\(\Leftrightarrow2x-3=1\)
\(\Leftrightarrow x=2\)

Bài 1:
a) \(2\sqrt{3}-5\sqrt{27}+3\sqrt{12}\)
\(=2\sqrt{3}-5\sqrt{3^2.3}+3\sqrt{2^2.3}\)
\(=2\sqrt{3}-5.3\sqrt{3}+3.2\sqrt{3}\)
\(=2\sqrt{3}-15\sqrt{3}+6\sqrt{3}\)
\(=-7\sqrt{3}\)
b) \(\frac{2+\sqrt{2}}{\sqrt{2}+1}:\frac{\sqrt{3}-1}{3-\sqrt{3}}\)
\(=\frac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}+1}.\frac{3-\sqrt{3}}{\sqrt{3}-1}\)
\(=\sqrt{2}.\frac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\)
\(=\sqrt{2}.\sqrt{3}\)
\(=\sqrt{6}\)
Bài 2:
a) \(T=\frac{a\sqrt{a}+1}{a-\sqrt{a}+1}-\frac{3a+\sqrt{a}}{\sqrt{a}}+\frac{a\sqrt{a}+a}{\sqrt{a}+1}\left(a>0\right)\)
\(=\frac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{a-\sqrt{a}+1}-\frac{\sqrt{a}\left(3\sqrt{a}+1\right)}{\sqrt{a}}+\frac{a\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\)
\(=\sqrt{a}+1-\left(3\sqrt{a}+1\right)+a\)
\(=a-2\sqrt{a}\)
b) Với \(T=-1\)
\(\Leftrightarrow a-2\sqrt{a}=-1\)
\(\Leftrightarrow a-2\sqrt{a}+1=0\)
\(\Leftrightarrow\left(\sqrt{a}-1\right)^2=0\)
\(\Leftrightarrow a=1\)

mình ko làm hộ bài thi giữa kì đâu nhé, đó là bài thi của bn mà
Bài 2 :
a, \(\sqrt{x-1}+\sqrt{4x-4}-\sqrt{25x-25}+2=0\)đk : x >= 1
\(\Leftrightarrow\sqrt{x-1}+2\sqrt{x-1}-5\sqrt{x-1}+2=0\Leftrightarrow-2\sqrt{x-1}=-2\)
\(\Leftrightarrow\sqrt{x-1}=1\Leftrightarrow x-1=1\Leftrightarrow x=2\)
b, \(\sqrt{\left(x-3\right)^2}=9\Leftrightarrow\left|x-3\right|=9\)
TH1 : \(x-3=9\Leftrightarrow x=12\)
TH2 : \(x-3=-9\Leftrightarrow x=-6\)
c, \(\sqrt{4x^2-4x+1}=x-1\Leftrightarrow\sqrt{\left(2x-1\right)^2}=x-1\Leftrightarrow\left|2x-1\right|=x-1\)
đk : x >= 1
TH1 : \(2x-1=x-1\Leftrightarrow x=0\)( ktm )
TH2 : \(2x-1=1-x\Leftrightarrow3x=2\Leftrightarrow x=\frac{2}{3}\)( ktm )
Vậy pt vô nghiệm







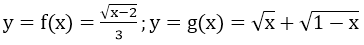
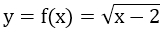 với x ≥ 2
với x ≥ 2