Do \(x_1,y_1\) lần lượt là các nghiệm của \(F\left(x\right)=ax+b\) và \(G\left(y\right)=cy+d\) nên ta có \(ax_1+b=cy_1+d=0\) (*)

 Mặt khác, \(ad=bc\Leftrightarrow\dfrac{a}{b}=\dfrac{c}{d}\). Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\left(k\ne0\right)\) thì suy ra \(a=kb;c=kd\). Thay vào (*), ta có \(kbx_1+b=kdy_1+d=0\) \(\Leftrightarrow b\left(kx_1+1\right)=d\left(ky_1+1\right)=0\) \(\Leftrightarrow kx_1+1=ky_1+1=0\) (do \(b,d\ne0\)) \(\Leftrightarrow x_1=y_1\) (đpcm)

Bạn nên viết đề bằng công toán (biểu tượng $\sum$ góc trái khung soạn thảo để được hỗ trợ tốt hơn. Đọc đề thế này khó dịch.

\(\dfrac{27}{23}\) + \(\dfrac{5}{21}\) - \(\dfrac{4}{23}\) + \(\dfrac{6}{21}\) + \(\dfrac{1}{2}\)

= (\(\dfrac{27}{23}\) - \(\dfrac{4}{23}\)) + (\(\dfrac{5}{21}\) + \(\dfrac{6}{21}\)) + \(\dfrac{1}{2}\)

= \(\dfrac{23}{23}\) + \(\dfrac{11}{21}\) + \(\dfrac{1}{2}\)

= 1 + \(\dfrac{11}{21}\) + \(\dfrac{1}{2}\)

= \(\dfrac{42}{42}\) + \(\dfrac{22}{42}\) + \(\dfrac{21}{42}\)

= \(\dfrac{85}{42}\)

Bài này có đúng là của lớp 7 không bạn?

A                    =  \(xy^2z^3\) + \(x^2y^3z^4\)+...+\(x^{2014}y^{2015}z^{2016}\) 

A \(\times\) \(xyz\)         =              \(x^2y^3z^4\)+...+\(x^{2014}y^{2015}z^{2016}\) + \(x^{2015}y^{2016}z^{2017}\)

A \(\times\) \(xyz\) - A    =     \(x^{2015}\)\(y^{2016}\)\(z^{2017}\) - \(xy^2z^3\) 

A\(\times\)( \(xyz\) - 1)  =    \(x^{2015}\)\(y^{2016}z^{2017}\) - \(xy^2z^3\)

A                   =  (\(x^{2015}\) \(y^{2016}\) \(z^{2017}\)   - \(xy^2z^3\)) : (\(xyz\) - 1)

Thay \(x\) = -1; \(y\) = -1; \(z\) = -1

A = [(-1)²⁰¹⁵.(-1)²⁰¹⁶.(-1)²⁰¹⁷ - (-1).(-1)².(-1)³] : {(-1.(-1).(-1) - 1)}

A = [ 1 - 1] : [-1-1]

A = 0: (-2)

A = 0

A                    =  $x{y}^2{z}^3$ + $x^2{y}^3{z}^4$+...+$x^{2014}{y}^{2015}{z}^{2016}$ 

A $\times$ $xyz$         =              $x^2{y}^3{z}^4$+...+$x^{2014}{y}^{2015}{z}^{2016}$ + $x^{2015}{y}^{2016}{z}^{2017}$

A $\times$ $xyz$ - A    =     $x^{2015}$$y^{2016}$$z^{2017}$ - $x{y}^2{z}^3$ 

A$\times$( $xyz$ - 1)  =    $x^{2015}$$y^{2016}{z}^{2017}$ - $x{y}^2{z}^3$

A                   =  ($x^{2015}$ $y^{2016}$ $z^{2017}$   - $x{y}^2{z}^3$) : ($xyz$ - 1)

Thay $x$ = -1; $y$ = -1; $z$ = -1

A = [(-1)2015.(-1)2016.(-1)2017 - (-1).(-1)2.(-1)3] : {(-1.(-1).(-1) - 1)}

A = [ 1 - 1] : [-1-1]

A = 0: (-2)

A = 0

Nhớ tick nha 

    A = 1³ + 2³ + 3³ + 4³ +...+ 100³

   Ta có:   B = 1³ + 2³ + 3³ + 4³ +...+ n³ = ( 1 + 2 + 3 +...+n)²

   Thật vậy Với n = 1 ta có: B = 1³ = 1² (đúng)

 Giả sử B đúng với n = k tức là:1³ + 2³ + 3³ +....+k³ = (1+2+3 +...+k)²

Ta cần chứng minh B  đúng với n = k + 1. 

⇔1³ + 2³ + 3³ + ...+ k³ + (k+1)³ = (1+2+3+...+k+k+1)² 

Ta có:

B = 1³ + 2³ + 3³ +....+ k³ + (k+1)³

B = (1+2+3+...+k)² + (k + 1)³

B = {(k +1)k:2}² + (k+1)³ = (k+1)²{ \(\dfrac{k^2}{4}\) + k + 1} =(k+1)²(k²+4k+4)²: 4

B = (k+1)²(k²+2k + 2k + 4): 4 = (k+1)²{(k(k+2) + 2(k+2)}: 4

B = (k+1)²(k+2)²:4 = {(k+1)(k+2): 2}²

Mặt khác 1 + 2 + 3 + 4 +....+ k + k + 1 = (k+2)(k+1): 2

⇒B = (1+2+3+...+ k+1)² (đpcm)

Vậy 1³ + 2³ + 3³ + ...+n³ = (1+2+3+...+n)² 

Áp dụng công thức trên ta có:

A = 1³ + 2³ + 3³ +4³ +...+100³ = (1+2+3+4...+100)²

C = 1 + 2 + 3 + 4 +...+100

Dãy số trên là dãy số cách đều với khoảng cách là 2 - 1 = 1

Số số hạng của dãy số trên là: (100 -1):1 + 1 = 100

Tổng dãy số trên là: C = (100 +1)\(\times\) 100  : 2 = 5050

A = 5050²

  A = 13 + 23 + 33 + 43 +...+ 1003

   Ta có:   B = 13 + 23 + 33 + 43 +...+ n3 = ( 1 + 2 + 3 +...+n)2

   Thật vậy Với n = 1 ta có: B = 13 = 12 (đúng)

 Giả sử B đúng với n = k tức là:13 + 23 + 33 +....+k3 = (1+2+3 +...+k)2

Ta cần chứng minh B  đúng với n = k + 1. 

⇔13 + 23 + 33 + ...+ k3 + (k+1)3 = (1+2+3+...+k+k+1)2 

Ta có:

B = 13 + 23 + 33 +....+ k3 + (k+1)3

B = (1+2+3+...+k)2 + (k + 1)3

B = {(k +1)k:2}2 + (k+1)3 = (k+1)2{ $\genfrac{}{}{0ex}{}{k^2}{4}$ + k + 1} =(k+1)2(k2+4k+4)2: 4

B = (k+1)2(k2+2k + 2k + 4): 4 = (k+1)2{(k(k+2) + 2(k+2)}: 4

B = (k+1)2(k+2)2:4 = {(k+1)(k+2): 2}2

Mặt khác 1 + 2 + 3 + 4 +....+ k + k + 1 = (k+2)(k+1): 2

⇒B = (1+2+3+...+ k+1)2 (đpcm)

Vậy 13 + 23 + 33 + ...+n3 = (1+2+3+...+n)2 

Áp dụng công thức trên ta có:

A = 13 + 23 + 33 +43 +...+1003 = (1+2+3+4...+100)2

C = 1 + 2 + 3 + 4 +...+100

Dãy số trên là dãy số cách đều với khoảng cách là 2 - 1 = 1

Số số hạng của dãy số trên là: (100 -1):1 + 1 = 100

Tổng dãy số trên là: C = (100 +1)$\times$ 100  : 2 = 5050

A = 50502

HT!

Câu 11 

Giá trị của biểu thức:A =  \(xy-2x^2y\) + 3\(xy\) + 2y\(x^2\) tại \(x\) = 1; \(y\) = \(-\dfrac{1}{2}\)

A = (\(xy\) + 3\(xy\)) - (2\(x^2y\) - 2\(yx^2\)) 

A = 4\(xy\) 

Thay \(x\) = 1; y = - \(\dfrac{1}{2}\) vào biểu thức A ta có:  

A = 4 \(\times\)1 \(\times\) ( - \(\dfrac{1}{2}\))

A = -2

Câu 9: Diện tích hình vuông là: \(x\) \(\times\) \(x\) = \(x^2\) (cm²)

           Diện tích hình chữ nhật là: \(x\times y\) = \(xy\) (cm²)

           Biểu thức biểu thị tổng diện tích của hình vuông và hình chữ nhật là:

               C.  \(x^2\) + \(xy\)

Bài 10: Thu gọn đa thức:

   \(xy\) - 2\(x^2\)y + 3\(xy\) + 2y\(x^2\)

= (\(xy\) + 3\(xy\)) - ( 2\(x^2\)y - 2y\(x^2\))

= 4\(xy\) - 0

Chọn C. 4\(xy\)

= 4\(xy\)

Hình ảnh như vậy chưa đủ cơ sở làm em hi

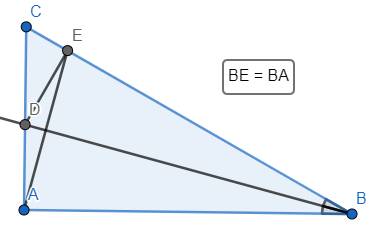
a) Xét ΔABD và ΔEBD có:

- BE = BA (giả thuyết)

- \(\widehat{ABD}=\widehat{EBD}\) (vì BD là tia phân giác của \(\widehat{ABC}\) )

- BD là cạnh chung

Suy ra ΔABD = ΔEBD (c.g.c)

b) Từ a) suy ra DE = AD (vì hai cạnh tương ứng) và \(\widehat{BAD}=\widehat{BED}=90^o\) (vì hai góc tương ứng), hay \(DE\perp BC\)

c) Từ BE = BA và DE = AD suy ra B và D đều nằm trên đường trung trực của AE, hay BD là đường trung trực của AE