\(3^{n+2}\) + \(3^{n+1}\) - \(3^n\) = 891
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số chân chó là:
\(128\times4=512\left(chan\right)\)
Số chân mèo:
\(128\times4=512\left(chan\right)\)
Tổng chân chó và chân mèo:
\(512+512=1024\left(chan\right)\)

vì mỗi con mèo có 4 cái chân nên
số chân của 33 con mèo là:
33×4 =132 ( cái )
Số chân của 33 con mèo là:
\(33\times4=132\left(chan\right)\)

B(x) = x2+x
Đặt B(x) = 0
=> x2+x=0
x.x + x = 0
x(x+1)=0
TH1: x = 0
TH2: x+1 = 0
x = -1
Vậy nghiệm của B(x) là x=-1

Cho n(x) = 0
5x² + 9x + 4 = 0
5x² + 5x + 4x + 4 = 0
(5x² + 5x) + (4x + 4) = 0
5x(x + 1) + 4(x + 1) = 0
(x + 1)(5x + 4) = 0
*) x + 1 = 0
x = 0 - 1
x = -1
*) 5x + 4 = 0
5x = 0 - 4
5x = -4
x = -4/5
Vậy nghiệm của đa thức n(x) là x = -1; x = -4/5
Cho \(n\left(x\right)=0\) \(\Leftrightarrow5x^2+9x+4=0\)
\(\Leftrightarrow5x^2+5x+4x+4=0\)
\(\Leftrightarrow5x\left(x+1\right)+4\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(5x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{4}{5}\end{matrix}\right.\)
Như vậy n(x) có 2 nghiệm là \(-1\) và \(-\dfrac{4}{5}\)

a, Tổng A có 11 số hạng
( Nhìn từ 21 đến 210 thấy được 10 số, thêm số 1 nữa => 11 số hạng )
b,
\(A=1+2^1+2^2+...+2^9+2^{10}\)
\(\Rightarrow2A=2+2^2+2^3+...+2^{10}+2^{11}\)
Ta có \(2A-A=\left(2+2^2+...+2^{11}\right)-\left(1+2^1+..+2^{10}\right)\)
\(\Leftrightarrow\)\(A\)\(=2^{11}-1\)
mà \(2^{11}-1< 2^{11}\)
hay \(A< 2^{11}\)
`@` `\text {Ans}`
`\downarrow`
`a,`
Số hạng của tổng A là:
`(10 - 1) \div 1 + 1 + 1 = 11 (\text {số hạng})`
`b,`
`A = 1+2^1+2^2+2^3+...+2^9+2^10`
`2A = 2(1+2+2^2+...+2^9+2^10)`
`2A = 2+2^2+2^3+...+2^10+2^11`
`2A - A = (2+2^2+2^3+...+2^10+2^11) - (1+2^1+2^2+2^3+...+2^9+2^10)`
`A = 2^11 - 1`
Vì `2^11 - 1 < 2^11`
`-> A < 2^11`
Vậy:
`a,` `11` số hạng *Mình dùng lũy thừa để tính á cậu;-;*
`b,` `A < 2^11.`

\(5^{n+1}+5^n=6\cdot125\)
`-> 5^n*5+5^n=750`
`-> 5^n(5+1)=750`
`-> 5^n*6=750`
`-> 5^n = 125`
`-> 5^n = 5^3`
`-> n=3`

Viết từ 1 đến 999 thì các số có chữ số ở hàng đơn vị có dạng:
\(\overline{a0}\); \(\overline{bc0}\).
Xét các số có dạng \(\overline{a0}\), \(a\) có 9 cách chọn vậy có 9 số
Xét các số có dạng \(\overline{bc0}\), \(b\) có 9 cách chọn; \(c\) có 10 cách chọn vậy có:
9 \(\times\) 10 = 90 (số)
Các số có chữ số 0 ở hàng chục có dạng: \(\overline{d0e}\)
\(d\) có 9 cách chọn. \(e\) có 10 cách chọn vậy có:
9 \(\times\) 10 = 90 (số)
Từ những lập trên cho thấy viết liên tiếp các số tự nhiên từ 1 đến 999 thì chữ số 0 xuất hiện số lần là:
9 + 90 + 90 = 189 (lần)
Đáp số: 189 lần
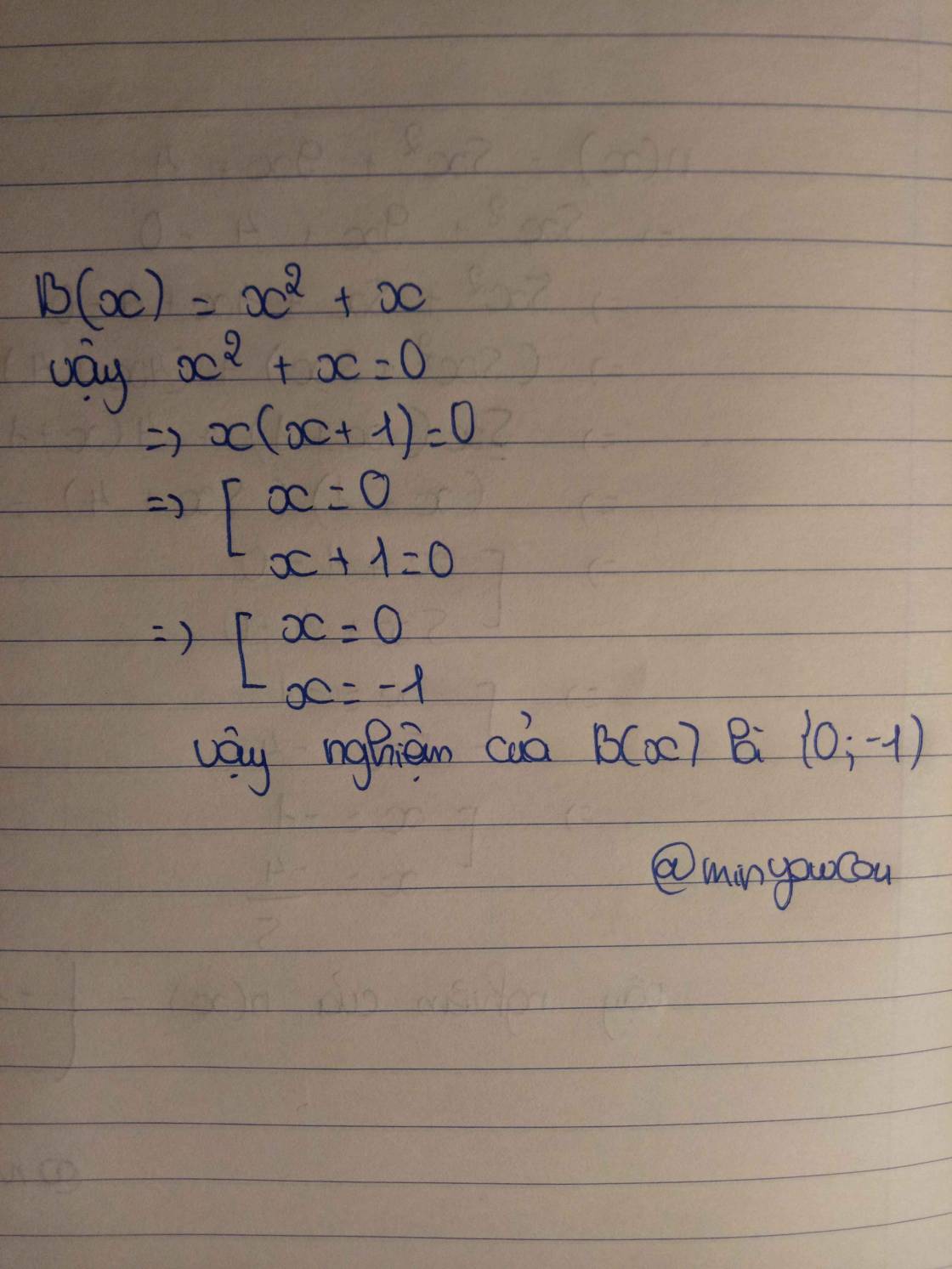
\(3^{n+2}+3^{n+1}-3^n=891\)
\(3^n\times3^2+3^n\times3-3^n=891\)
\(3^n\times\left(9+3-1\right)=891\)
\(3^n\times11=891\)
\(3^n=891\div11\)
\(3^n=81\)
\(3^n=3^4\)
\(n=4\)
\(3^{n+2}+3^{n+1}-3^n=891\)
\(\Leftrightarrow3^n.3^2+3^n.3-3^n=891\)
\(\Leftrightarrow3^n\left(3^2+3-1\right)=891\)
\(\Leftrightarrow3^n.11=891\)
\(\Leftrightarrow3^n=81\)
\(\Rightarrow n=4\)