Tìm số tự nhiên thỏa mãn: .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$3+2^{x-1}=24-[4^2-(2^2-1)]=24-(16-3)=24-13=11$
$2^{x-1}=11-3=8=2^3$
$\Rightarrow x-1=3$
$\Rightarrow x=4$

Lời giải:
$1-4+7-10+...+2017-2020$
$=(1-4)+(7-10)+....+(2017-2020)$
$=\underbrace{(-3)+(-3)+....+(-3)}_{337}=337\times (-3)=-1011$

a) ( -2x - 28 )5 = -32 = ( -2 )5
-2x - 28 = -2
-2x = ( -2 ) + 28 = 26
x = 26 : ( -2 ) = -13
b) ( 7x - 11 )3 = 1000 = 103
7x - 11 = 10
7x = 10 + 11 = 21
x = 21 : 7 = 3
c) ( 3x - 15 )2 - 6 = 75
( 3x - 15 )2 = 75 + 6 = 81 = 92
3x - 15 = 9
3x = 9 + 15 = 24
x = 24 : 3 = 8



P=1/3+1/15+1/35+1/63+1/99
=1:3+1:15+1:35+1:63+1:99
=1:(3+15+35+63+99)
=1:215
=1/215
Vậy:P=1/215


Gọi 2 số cần tìm là \(a,b\left(a>b\right)\), ta có:
\(a+b=102\)
\(a+10b=417\)
\(\Rightarrow9b=\left(a+10b\right)-\left(a+b\right)\)
\(\Rightarrow9b=417-102=315\)
\(\Rightarrow b=315:9=35\)
Mà \(a+b=102\) nên \(a=102-b=102-35=67\)
Vậy số lớn là 67
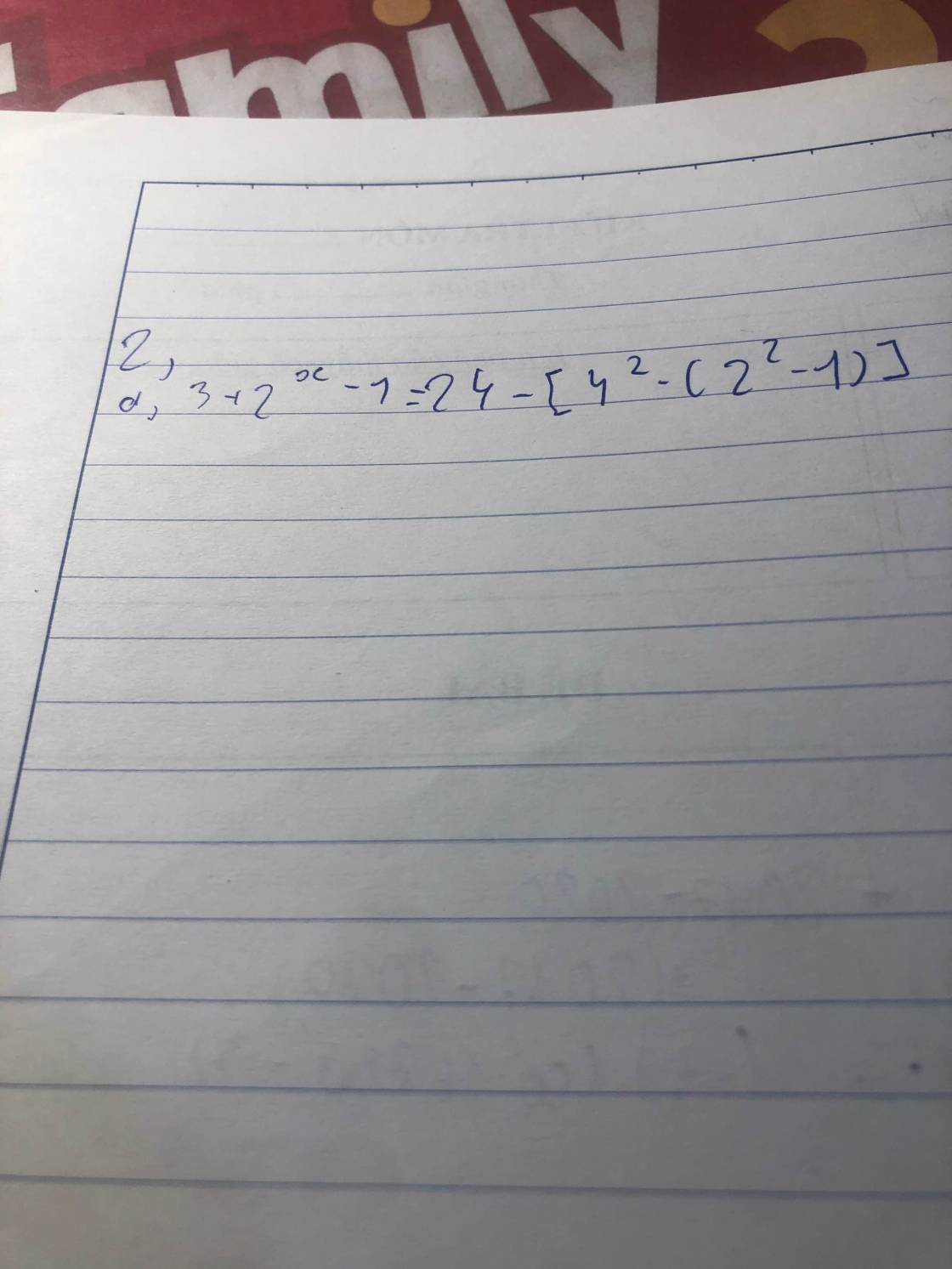

Lời giải:
$(3x+2)^2=121=11^2=(-11)^2$
$\Rightarrow 3x+2=11$ hoặc $3x+2=-11$
$\Rightarrow x=3$ hoặc $x=\frac{-13}{3}$
Vì $x$ là số tự nhiên nên $x=3$