3457 - 27 x 48 - 48 x 73 + 6543
tính nhanh giúp mình nhé
iiuiuuiuuuiuuuuiuuuuu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B = 13 + 23 + 33 +....+ n3
B = ( 1+2+3+...+n)2
Với B = 1 ta có 13 = 12 đúng
Giả sử B đúng với n= k tức là:
13 + 23 + 33+...+ k3=(1+2+...+k)2 (đúng)
Ta cần chứng minh B đúng với n = k + 1
Tức là Chứng minh:
13 + 23 + 33 +...+ k3 + (k+1)3 = ( 1+2+...+k+1)2
Thật vậy ta có:
B = 13 + 23 + 33 +...+ k3 + (k+1)3
B = (1+2+3+...+k)2 +(k+1)3
B = [ k(k+1):2]2 + (k+1)3
B = (k+1)2[ \(\dfrac{k^2}{4}\) + k + 1] = (k+1)2[ k2 +4k +4]:4
B = (k+1)2[ k2+2k +2k+ 4] :4
B = (k+1)2[ k(k +2) + 2(k+2)]:4
B = (k+1)2(k+2)(k+2):4
B = {(k+1)(k+2) : 2}2
Mặt khác ta cũng có:
1 + 2 + 3 + 4 +...+ k+ k+ 1 = (k+1+1)(k+1):2 = (k+1)(k+2):2
⇔ B = (1+2+3+...+k+1)2(đpcm)
Vậy B = 13 +23 + 33 +...+n3 = (1+2+3+...+n)2
Toán lớp 5 chưa học cái này nha bạn
Lớp 5 chia học mũ lên lớp 6 mới học

A = 1.2 + 2.3 +...+ n.(n+1)
1.2.3 = 1.2.3
2.3.3 = 2.3.( 4-1) = 2.3.4 - 1.2.3
3.4.3 = 3.4(5-2) = 3.4.5 - 2.3.4
.................................................
n(n+1).3 =n(n+1)[ (n+2) - (n-1)] = n(n+1)(n+2) - (n-1)n(n+1)
Cộng vế với vế ta có:
1.2.3+2.3.3+...+n(n+1).3 = n(n+1)(n+2)
3.[1.2+ 2.3+...+ n(n+1)] = n(n+1)(n+2)
1.2 + 2.3 +...+n(n+1) = n(n+1)(n+2): 3
A = 1.2 + 2.3 +...+ n.(n+1)
1.2.3 = 1.2.3
2.3.3 = 2.3.( 4-1) = 2.3.4 - 1.2.3
3.4.3 = 3.4(5-2) = 3.4.5 - 2.3.4
.................................................
n(n+1).3 =n(n+1)[ (n+2) - (n-1)] = n(n+1)(n+2) - (n-1)n(n+1)
Cộng vế với vế ta có:
1.2.3+2.3.3+...+n(n+1).3 = n(n+1)(n+2)
3.[1.2+ 2.3+...+ n(n+1)] = n(n+1)(n+2)
1.2 + 2.3 +...+n(n+1) = n(n+1)(n+2): 3
HT!

A =1.2 + 2.3 + ....+ n.(n+1)
A = n(n+1) + ....+ 2.3 + 1.2
A\(\times\) 3 = n(n+1).3 +....+ 2.3.3+ 1.2.3
A\(\times\)3 = n(n+1)[n+2 - (n -1)]+....+2.3.(4-1) +1.2.3
A\(\times\)3 = n(n+1)(n+2) - (n-1)n(n+1) +....+ 2.3.4 - 1.2.3 + 1.2.3
A\(\times\)3 = n(n+1)(n+2)
A \(\times\)3 = n(n+1)(n+2)
A = n(n+1)(n+2) : 3

Số thứ nhất = 75% Số thứ 2
Tức là số thứ nhất = 3/4 Số thứ hai
Tổng số phần bằng nhau:
3+4=7(phần)
Số thứ nhất là:
847 : 7 x 3= 363
Số thứ hai là:
847:7 x 4= 484
75% = \(\dfrac{3}{4}\)
Theo bài ra ta có sơ đồ:
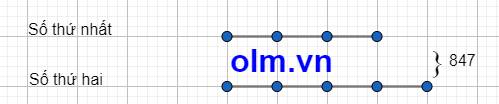
Theo sơ đồ ta có:
Số thứ nhất là: 847 : ( 3 + 4) \(\times\) 3 = 363
Số thứ hai là: 847 - 363 = 484
Đáp số: Số thứ nhất là 363
Số thứ hai là 484

A = 13 + 23 + 33 + 43 +...+ 1003
Ta có: B = 13 + 23 + 33 + 43 +...+ n3 = ( 1 + 2 + 3 +...+n)2
Thật vậy Với n = 1 ta có: B = 13 = 12 (đúng)
Giả sử B đúng với n = k tức là:13 + 23 + 33 +....+k3 = (1+2+3 +...+k)2
Ta cần chứng minh B đúng với n = k + 1.
⇔13 + 23 + 33 + ...+ k3 + (k+1)3 = (1+2+3+...+k+k+1)2
Ta có:
B = 13 + 23 + 33 +....+ k3 + (k+1)3
B = (1+2+3+...+k)2 + (k + 1)3
B = {(k +1)k:2}2 + (k+1)3 = (k+1)2{ \(\dfrac{k^2}{4}\) + k + 1} =(k+1)2(k2+4k+4)2: 4
B = (k+1)2(k2+2k + 2k + 4): 4 = (k+1)2{(k(k+2) + 2(k+2)}: 4
B = (k+1)2(k+2)2:4 = {(k+1)(k+2): 2}2
Mặt khác 1 + 2 + 3 + 4 +....+ k + k + 1 = (k+2)(k+1): 2
⇒B = (1+2+3+...+ k+1)2 (đpcm)
Vậy 13 + 23 + 33 + ...+n3 = (1+2+3+...+n)2
Áp dụng công thức trên ta có:
A = 13 + 23 + 33 +43 +...+1003 = (1+2+3+4...+100)2
C = 1 + 2 + 3 + 4 +...+100
Dãy số trên là dãy số cách đều với khoảng cách là 2 - 1 = 1
Số số hạng của dãy số trên là: (100 -1):1 + 1 = 100
Tổng dãy số trên là: C = (100 +1)\(\times\) 100 : 2 = 5050
A = 50502
A = 13 + 23 + 33 + 43 +...+ 1003
Ta có: B = 13 + 23 + 33 + 43 +...+ n3 = ( 1 + 2 + 3 +...+n)2
Thật vậy Với n = 1 ta có: B = 13 = 12 (đúng)
Giả sử B đúng với n = k tức là:13 + 23 + 33 +....+k3 = (1+2+3 +...+k)2
Ta cần chứng minh B đúng với n = k + 1.
⇔13 + 23 + 33 + ...+ k3 + (k+1)3 = (1+2+3+...+k+k+1)2
Ta có:
B = 13 + 23 + 33 +....+ k3 + (k+1)3
B = (1+2+3+...+k)2 + (k + 1)3
B = {(k +1)k:2}2 + (k+1)3 = (k+1)2{ + k + 1} =(k+1)2(k2+4k+4)2: 4
B = (k+1)2(k2+2k + 2k + 4): 4 = (k+1)2{(k(k+2) + 2(k+2)}: 4
B = (k+1)2(k+2)2:4 = {(k+1)(k+2): 2}2
Mặt khác 1 + 2 + 3 + 4 +....+ k + k + 1 = (k+2)(k+1): 2
⇒B = (1+2+3+...+ k+1)2 (đpcm)
Vậy 13 + 23 + 33 + ...+n3 = (1+2+3+...+n)2
Áp dụng công thức trên ta có:
A = 13 + 23 + 33 +43 +...+1003 = (1+2+3+4...+100)2
C = 1 + 2 + 3 + 4 +...+100
Dãy số trên là dãy số cách đều với khoảng cách là 2 - 1 = 1
Số số hạng của dãy số trên là: (100 -1):1 + 1 = 100
Tổng dãy số trên là: C = (100 +1) 100 : 2 = 5050
A = 50502
HT!

Bài 8:
Chiều dài ban đầu của thửa ruộng hình chữ nhật là:
500 : 5 = 100 (m)
Chiều rộng ban đầu của thửa ruộng hình chữ nhật là:
375 : 100 = 3,75 (m)
Chu vi của thửa ruộng ban đầu là:
(100 + 3,75) \(\times\) 2 = 207,5 (m)
Đáp số: 207,5 m

Lời giải:
Lần đầy 4 xe chuyển được số muối là:
$3\times 4=12$ (tấn) ($=120$ tạ)
Cả hai lần chở được số muối là:
$120+25=145$ (tạ)
Số muối lần đầu 4 xe chở được là:
3 \(\times\) 4 = 12 (tấn)
Số muối lần sau 4 xe chở được là:
25 \(\times\) 4 = 100 (tạ)
Đổi 100 tạ = 10 tấn
Cả hai lần chở được số muối là:
12 + 10 = 22 (tấn)
Đáp số: 22 tấn

Trường hợp xấu nhất sẽ bốc phải:
12 bi màu tím + 10 viên bi đỏ = 22 ( viên bi)
Dể chắc chắn có đủ cả 3 màu bi thì cần bốc ít nhất số bi là:
22 + 1 = 23 ( viên bi)
Đáp số: 23 viên bi.
Số viên Sơn phải lấy để có đủ cả 4 màu bi là:
8 + 10 + 4 = 22 ( viên bi )
Đáp số : 22 viên bi
A = 3457 - 27\(\times\) 48 - 48 \(\times\) 73 + 6543
A =(3457 + 6543) - ( 27 \(\times\) 48 + 48 \(\times\) 73)
A = 10 000 - 48 \(\times\) ( 27 + 73)
A = 10 000 - 48 \(\times\) 100
A = 100 \(\times\) ( 100 - 48)
A = 100 \(\times\) 52
A = 5200
A = 3457 - 27×× 48 - 48 ×× 73 + 6543
A =(3457 + 6543) - ( 27 ×× 48 + 48 ×× 73)
A = 10 000 - 48 ×× ( 27 + 73)
A = 10 000 - 48 ×× 100
A = 100 ×× ( 100 - 48)
A = 100 ×× 52
A = 5200
HT!