Tìm $x$, biết $|\sqrt x - 1| - 3 = 1$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = |x-y| + |x+1| + 2016
|x-y| ≥ 0 ; |x+1| ≥ 0 ⇔ |x-y| + |x+1| +2016 ≥ 2016
⇔ A(min)= 2016 ⇔ y= x = -1;
\(A=\left|x-y\right|+\left|x+1\right|+2016\ge2016\)
Dấu ''='' xảy ra khi x = y = -1

a, \(\left|x+6\right|+2\ge2\Rightarrow\dfrac{1}{\left|x+6\right|+2}\le\dfrac{1}{2}\)
Dấu ''='' xảy ra khi x = -6



Với x >= 0 ; x khác 4
\(P=\dfrac{2\left(\sqrt{x}-2\right)+5}{\sqrt{x}-2}=2+\dfrac{5}{\sqrt{x}-2}\Rightarrow\sqrt{x}-2\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
| \(\sqrt{x}-2\) | 1 | -1 | 5 | -5 |
| x | 9 | 1 | 49 | loại |

A = \(\sqrt{36}\).( 3\(\sqrt{4}\) - \(\sqrt{\dfrac{1}{9}}\)) + 2
A = 6( 3.2- \(\dfrac{1}{3}\)) + 2
A = 6.3.2 - 2 + 2
A = 36
B = \(\sqrt{\dfrac{1}{9}+\dfrac{1}{16}}\)
B = \(\sqrt{\dfrac{25}{9.16}}\)
B = 5/12
C = ( \(\sqrt{\dfrac{1}{9}}\)+ \(\sqrt{\dfrac{25}{36}}\)- \(\sqrt{\dfrac{49}{81}}\)): \(\sqrt{\dfrac{441}{324}}\)
C = ( 1/3+ 5/6 - 7/9) : 7/6
C = ( 6/18 +15/18 -14/18): 7/6
C = 7/18 : 7/6
C = 7/18 .6/7
C = 1/3
D =\(\sqrt{(\dfrac{-2}{5})^2}\)+ \(\sqrt{1,44}\) - \(\sqrt{256}\)
D = 2/5 + 1,2 - 16
D = 0,4 + 1,2 - 16
D = -14,4

chứng minh bằng phương pháp phản chứng
giả sử \(\sqrt{\dfrac{1}{3}}\) là số hữu tỉ thì ta có
\(\sqrt{\dfrac{1}{3}}\) = \(\dfrac{a}{b}\) \(\Leftrightarrow\) 1/3 = \(\dfrac{a^2}{b^2}\)
⇔ a2 = 1; b2 = 3
vì b là số tự nhiên nên b2 là một số chính phương
mà một số chính phương không thể có tận cùng bằng 3 . ⇒ b#3
từ lập luận trên cho thấy điều giả sử là sai vậy \(\sqrt{\dfrac{1}{3}}\) là số vô tỉ

\(\sqrt{7}-\sqrt{3}\)
Giả sử \(\sqrt{7}-\sqrt{3}\) = m ( m là số hữu tỉ ), ta có :
=>( \(\sqrt{7}-\sqrt{3}\) )2 => m2 = 7 + \(\sqrt{3}\) = m2 => \(\sqrt{3}\) = m2 - 7
Vì m là số hữu tỉ nên m2 là số hữu , do đó m2 - 7 cũng là số hữu tỉ.
=> \(\sqrt{3}\) là số vô tỉ ( vô lý vì \(\sqrt{3}\) là số hữu tỉ )
Như vậy:
=> Giả sử sai : \(\sqrt{7}-\sqrt{3}\) là số vô tỉ ( ĐPCM )
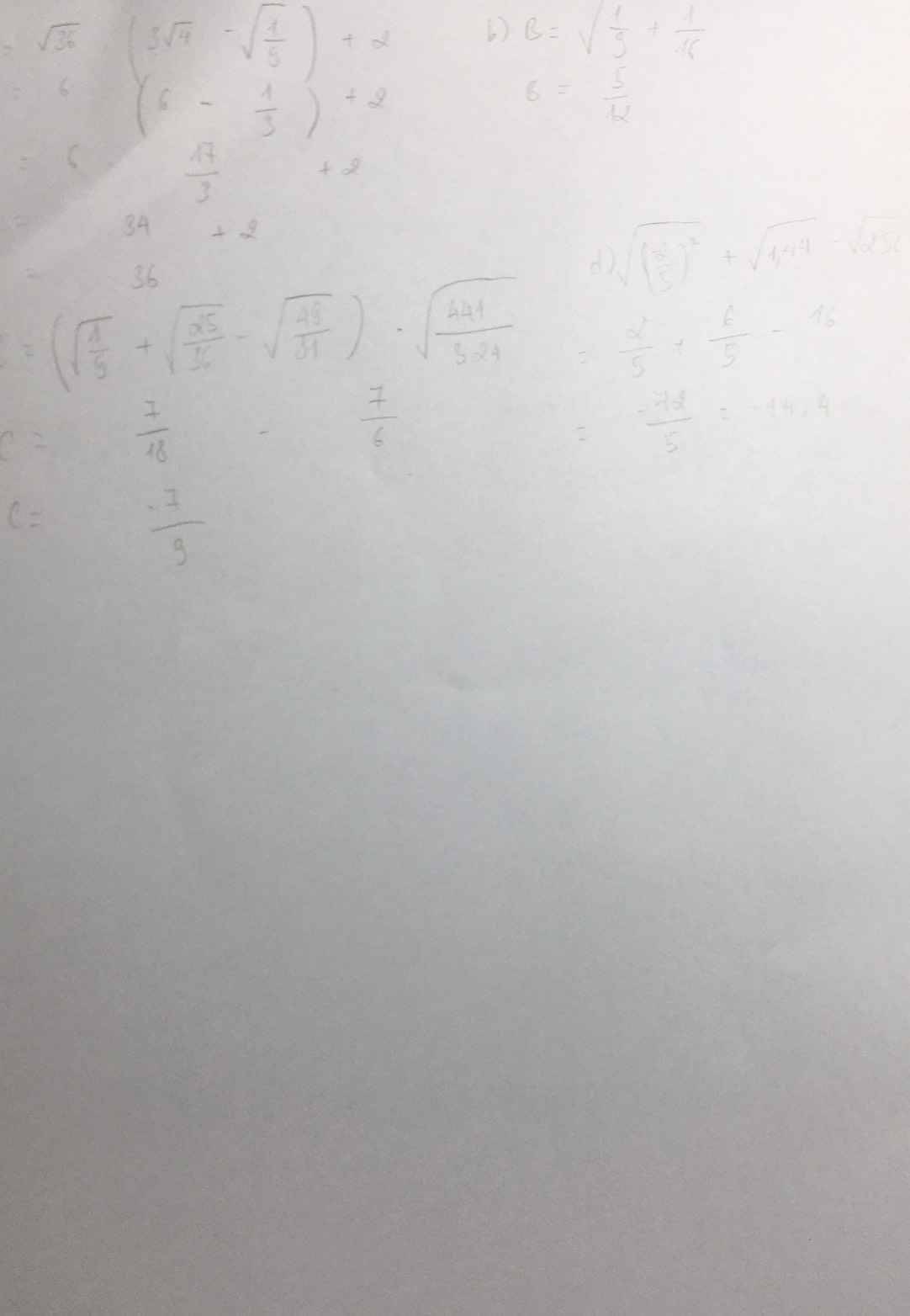
đk x> =0
\(\left|\sqrt{x}-1\right|=4\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-1=4\\\sqrt{x}-1=-4\end{matrix}\right.\Leftrightarrow x=25\)
| \(\sqrt{x}\) - 1| - 3 = 1 (đk x >0)
|\(\sqrt{x}\) - 1| = 1 + 3
|\(\sqrt{x}\) - 1| = 4
\(\sqrt{x}\) - 1 = +-4
\(\sqrt{x}\) = 5; \(\sqrt{x}\) = -3 (loại)
\(\sqrt{x}\) = 5 ⇔ x = 25