P nguyên <=> \(\dfrac{x-5}{\sqrt{x}+1}\) nguyên

<=> \(\dfrac{x-1}{\sqrt{x}+1}-\dfrac{4}{\sqrt{x}+1}\) nguyên

<=> \(\sqrt{x}-1-\dfrac{4}{\sqrt{x}+1}\) nguyên

=> \(\sqrt{x}+1\inƯ\left(4\right)=\left\{1;2;4\right\}\)  (vì \(\sqrt{x}+1>0\forall x\in N\))

...

Thời gian đoàn tàu chạy qua cây cầu bằng thời gian đoàn tàu đi hết chiều dài cây cầu và chiều dài của đoàn tàu.

Đoàn tàu đi hết quãng đường 450 mét sau:

65 giây - 20 giây = 45 giây

Vận tốc đoàn tàu là:

450 : 45  = 10(m/s)

Chiều dài đoàn tàu là:

10 \(\times\) 20 = 200 (m)

Đáp số: Chiều dài đoàn tàu là 200 m

            Vận tốc đoàn tàu là 10m/s 

Đoàn tàu đi hết quãng đường 450 mét sau:

65 giây - 20 giây = 45 giây

Vận tốc đoàn tàu là:

450 : 45  = 10(m/s)

Chiều dài đoàn tàu là:

10 $\times$ 20 = 200 (m)

Đáp số: Chiều dài đoàn tàu là 200 m

            Vận tốc đoàn tàu là 10m/s 

Cùng một quãng đường vận tốc và thời gian là hai đại lượng tỉ lệ nghịch.

Tỉ số vận tốc thời gian đi và thời gian về là:

      20: 12 = \(\dfrac{5}{3}\) 

Ta có sơ đồ: 

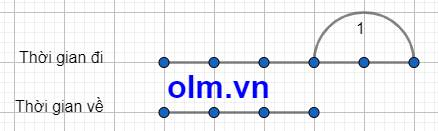
Theo sơ đồ ta có:

Thời gian đi là: 1:(5-3) \(\times\) 5 = 2,5 (giờ)

Quãng đường AB dài là:

12 \(\times\)2,5 = 30 (km)

Đáp số: 30 km

Hướng dẫn: Bài toán Tỉ lệ nghịch và hiệu tỉ

Cùng quãng đường AB nên thời gian và vận tốc tỉ lệ nghịch với nhau

Tỉ số thời gian về với thời gian đi là:

12: 20 = 3: 5 

Thời gian về là:

1: (5-3)x3 = 1,5 (giờ)

Quãng đường AB là:

20 x 1,5 = 30 (km)

Đáp số: 30 km

Độ dài đáy DC là:18 x 3 = 54 (cm)

a) Diện tích hình thang ABCD là: 

(18 + 54) x 12 : 2 = 432 (cm²)

b) Vì có chung độ dài chiều cao và tỉ số \(\dfrac{AB}{DC}=\dfrac{1}{3}\) , ta kết luận rằng diện tích DBC lớn hơn và gấp 3 lần diện tích ADB.

10% = \(\dfrac{1}{10}\) 

6 300 000 đồng ứng với phân số là:

   1 - \(\dfrac{1}{5}\) - \(\dfrac{1}{10}\) = \(\dfrac{7}{10}\) ( lương tháng 6)

Lương tháng 6 của mẹ An là:

    6 300 000 : \(\dfrac{7}{10}\) = 9 000 000 (đồng)

Đáp số: 9 000 000 đồng

Số tiền mẹ bạn An đã chi tiêu tương đương với:

\(\dfrac{1}{5}+10\%=30\%\) (lương tháng 6)

Lương tháng 6, mẹ An nhận được số tiền là:

6 300 000 : (100 - 30) x 100 = 9 000 000 (đồng)

Đáp số: 9 000 000 đồng

Đổi 1 giờ 30 phút = 1,5 giờ

Khi xe taxi khởi hành thì xe taxi và xe máy cách nhau:

          48 \(\times\) 1,5 = 72 (km)

Thời gian hai xe gặp nhau là:

          72: ( 72 - 48) =3 ( giờ)

Vị trí hai xe gặp nhau cách A là:

           72 \(\times\) 3  = 216 ( km)

Đáp số: 216 km 

Đổi 1 giờ 30 phút = 1,5 giờ

Khi xe taxi khởi hành thì xe taxi và xe máy cách nhau:

          48 $\times$ 1,5 = 72 (km)

Thời gian hai xe gặp nhau là:

          72: ( 72 - 48) =3 ( giờ)

Vị trí hai xe gặp nhau cách A là:

           72 $\times$ 3  = 216 ( km)

Đáp số: 216 km 

Số ban đầu cộng với số mới bằng 34362

Số ban đầu trừ 9 gấp 10 lần số mới

Bài toán Tổng tỉ

Số mới là:

(34362 - 9): (10+1) =3123

Số cần tìm là: 31239

gọi số cần tìm là : abcde 
theo đề ta có : abcd9 + abcd = 34362
=> abcd x 10 + 9 + abcd = 34362
=> abcd x (10 + 1) = 34362 -9
=> abcd x 11 = 34353
=> abcd = 34353 : 11 
=> abcd = 3123
Vậy số tự nhiên đó là 3123
 

Lời giải:

Số số hạng: $(95-15):10+1=9$ (số)

Giá trị của tổng trên: $(95+15)\times 9:2=495$ 

Lời giải:

Tổng chiều dài và chiều rộng: $170:2=85$ (m) 

Tổng chiều dài và chiều rộng khi chiều dài thêm 5m: $85+5=90$ (m) 

Chiều rộng là: $90:(1+2)\times 1=30$ (m) 

Chiều dài là: $85-30=55$ (m)

Diện tích khu đất: $30\times 55=1650$ (m²)

A = \(\dfrac{2}{3}\) + \(\dfrac{3}{18}\) + \(\dfrac{1}{42}\) + \(\dfrac{2}{63}\) + \(\dfrac{3}{108}\)

A = \(\dfrac{2}{1\times3}\) + \(\dfrac{3}{3\times6}\) + \(\dfrac{1}{6\times7}\)+ \(\dfrac{2}{7\times9}\) + \(\dfrac{3}{9\times12}\)

A = \(\dfrac{1}{1}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{6}\) + \(\dfrac{1}{6}\) - \(\dfrac{1}{7}\) + \(\dfrac{1}{7}\) - \(\dfrac{1}{9}\) + \(\dfrac{1}{9}\) - \(\dfrac{1}{12}\)

A = 1 - \(\dfrac{1}{12}\)

A = \(\dfrac{11}{12}\)