Cho phương trình ( là tham số). Tìm m để phương trình đã cho có hai nghiệm phân biệt
( là tham số). Tìm m để phương trình đã cho có hai nghiệm phân biệt 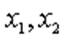 thỏa mãn
thỏa mãn 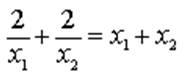
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Để pt có 2 nghiệm phân biệt thì $\Delta'=1-(m-3)>0$
$\Leftrightarrow 4-m>0\Leftrightarrow m< 4$
Áp dụng định lý Viet:
$x_1+x_2=2$
$x_1x_2=m-3$
Khi đó:
$x_1^2-(x_1+x_2)x_2+x_1x_2=-12$
$\Leftrightarrow x_1^2-x_2^2=-12$
$\Leftrightarrow (x_1-x_2)(x_1+x_2)=-12$
$\Leftrightarrow 2(x_1-x_2)=-12$
$\Leftrightarrow x_1-x_2=-6$
Kết hợp với $x_1+x_2=2$ thì $x_1=-2; x_2=4$
$m-3=x_1x_2=(-2).4=-8$
$\Leftrightarrow m=-5$ (tm)

Ta có \(x^2+y^2=1\Leftrightarrow\left(x+y\right)^2=2xy+1\)
Từ đó \(P=\dfrac{\left(x+y\right)^2}{x+y+1}\). Đặt \(x+y=t\left(t\ge0\right)\). Vì \(x+y\le\sqrt{2\left(x^2+y^2\right)}=2\) nên \(t\le\sqrt{2}\). ĐTXR \(\Leftrightarrow x=y=\dfrac{1}{\sqrt{2}}\). Ta cần tìm GTLN của \(P\left(t\right)=\dfrac{t^2}{t+1}\) với \(0\le t\le\sqrt{2}\).
Giả sử có \(0\le t_1\le t_2\le\sqrt{2}\). Ta có BDT luôn đúng \(\left(t_2-t_1\right)\left(t_2+t_1+t_2t_1\right)\ge0\) \(\Leftrightarrow t_2^2-t_1^2+t_2^2t_1-t_2t_1^2\ge0\) \(\Leftrightarrow t_1^2\left(t_2+1\right)\le t_2^2\left(t_1+1\right)\) \(\Leftrightarrow\dfrac{t_1^2}{t_1+1}\le\dfrac{t_2^2}{t_2+1}\) \(\Leftrightarrow P\left(t_1\right)\le P\left(t_2\right)\). Như vậy với \(0\le t_1\le t_2\le\sqrt{2}\) thì \(P\left(t_1\right)\le P\left(t_2\right)\). Do đó P là hàm đồng biến. Vậy GTLN của P đạt được khi \(t=\sqrt{2}\) hay \(x=y=\dfrac{1}{\sqrt{2}}\), khi đó \(P=2\sqrt{2}-2\)
Lời giải:
$P=\frac{2xy+1}{x+y+1}=\frac{2xy+x^2+y^2}{x+y+1}=\frac{(x+y)^2}{x+y+1}$
$=\frac{a^2}{a+1}$ với $x+y=a$
Áp dụng BĐT AM-GM:
$1=x^2+y^2\geq \frac{(x+y)^2}{2}=\frac{a^2}{2}$
$\Rightarrow a^2\leq 2\Rightarrow a\leq \sqrt{2}$
$P=\frac{a^2}{a+1}=\frac{a}{1+\frac{1}{a}}$
Vì $a\leq \sqrt{2}\Rightarrow 1+\frac{1}{a}\geq 1+\frac{1}{\sqrt{2}}=\frac{2+\sqrt{2}}{2}$
$\Rightarrow P\leq \frac{\sqrt{2}}{\frac{2+\sqrt{2}}{2}}=-2+2\sqrt{2}$
Vậy $P_{\max}=-2+2\sqrt{2}$ khi $x=y=\frac{1}{\sqrt{2}}$

a,
Xét pt hoành độ giao điểm của (P) và (d): \(x^2+2x-2m=0\) (1)
\(\Delta=2^2-4\left(-2m\right)=4+8m\)
Để (d) tiếp xúc (P) thì pt (1) có nghiệm kép \(\Rightarrow\Delta=4+8m=0\)
\(\Rightarrow m=-\dfrac{1}{2}\)
Thay \(m=-\dfrac{1}{2}\) vào (1) \(\Rightarrow x^2+2x+1=0\)
\(\Rightarrow\left(x+1\right)^2=0\) \(\Rightarrow x=-1\)
\(\Rightarrow y=\dfrac{1}{2}\left(-1\right)^2=\dfrac{1}{2}\)
Vậy (d) tiếp xúc (P) khi \(m=-\dfrac{1}{2}\) tại tọa độ \(\left(-1;\dfrac{1}{2}\right)\).
Lời giải:
Để pt có 2 nghiệm phân biệt thì:
$\Delta'=m^2-(m^2+2m+2)>0$
$\Leftrightarrow 2m+2<0$
$\Leftrightarrow m< -1$
Áp dụng định lý Viet, với $x_1,x_2$ là nghiệm thì:
$x_1+x_2=2m$
$x_1x_2=m^2+2m+2$
$m^2+2m+2=(m+1)^2+1>0$ nên $x_1,x_2$ luôn khác $0$
Khi đó:
$\frac{2}{x_1}+\frac{2}{x_2}=x_1+x_2$
$\Leftrightarrow 2.\frac{x_1+x_2}{x_1x_2}=x_1+x_2$
$\Leftrightarrow 2.\frac{2m}{m^2+2m+2}=2m$
$\Leftrightarrow 2m(\frac{2}{m^2+2m+2}-1)=0$
$\Leftrightarrow m=0$ hoặc $m^2+2m+2=2$
$\Leftrightarrow m=0$ hoặc $m(m+2)=0$
$\Leftrightarrow m=0$ hoặc $m=-2$ Vì $m< -1$ nên $m=-2$