0,25x7/15-1/4x-8/15+2,75
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


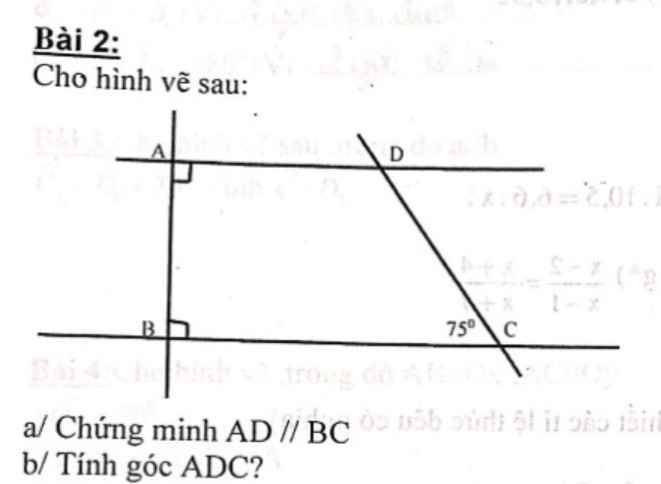
\(a,\) Ta có : \(\left\{{}\begin{matrix}AD\perp AB\left(gt\right)\\BC\perp AB\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow AD//BC\) ( cùng vuông góc với \(AB\) )
\(b,\) Ta có tứ giác thì 4 góc là \(360^o\)
\(\Rightarrow\widehat{ADC}=360^o-\widehat{BAD}-\widehat{ABC}-\widehat{DCB}\)
\(=360^o-90^o-90^o-75^o=105^o\)
Vậy \(\widehat{ADC}=105^o\)

\(a,\left(7+3\dfrac{1}{4}-\dfrac{3}{5}\right)+\left(0,4-5\right)-\left(4\dfrac{1}{4}-1\right)\)
\(=\left(7+\dfrac{13}{4}-\dfrac{3}{5}\right)-\dfrac{23}{5}-\left(\dfrac{17}{4}-1\right)\)
\(=7+\dfrac{13}{4}-\dfrac{3}{5}-\dfrac{23}{5}-\dfrac{17}{4}+1\)
\(=\left(7+1\right)+\left(\dfrac{13}{4}-\dfrac{17}{4}\right)-\left(\dfrac{3}{5}+\dfrac{23}{5}\right)\)
\(=8-\dfrac{4}{4}-\dfrac{26}{5}\)
\(=7-\dfrac{26}{5}\)
\(=\dfrac{9}{5}\)
\(b,\dfrac{2}{3}-\left[\left(-\dfrac{7}{4}\right)-\left(\dfrac{1}{2}+\dfrac{3}{8}\right)\right]\)
\(=\dfrac{2}{3}-\left(-\dfrac{7}{4}-\dfrac{1}{2}-\dfrac{3}{8}\right)\)
\(=\dfrac{2}{3}-\left(-\dfrac{14}{8}-\dfrac{4}{8}-\dfrac{3}{8}\right)\)
\(=\dfrac{2}{3}-\left(-\dfrac{21}{8}\right)\)
\(=\dfrac{2}{3}+\dfrac{21}{8}\)
\(=\dfrac{79}{24}\)
\(c,\left(9-\dfrac{1}{2}-\dfrac{3}{4}\right):\left(7-\dfrac{1}{4}-\dfrac{5}{8}\right)\)
\(=\left(\dfrac{36}{4}-\dfrac{2}{4}-\dfrac{3}{4}\right):\left(\dfrac{56}{8}-\dfrac{2}{8}-\dfrac{5}{8}\right)\)
\(=\dfrac{31}{4}:\dfrac{49}{8}\)
\(=\dfrac{62}{49}\)
\(d,3-\dfrac{1-\dfrac{1}{7}}{1+\dfrac{1}{7}}=3-\dfrac{\dfrac{7}{7}-\dfrac{1}{7}}{\dfrac{7}{7}+\dfrac{1}{7}}=3-\left(\dfrac{6}{7}:\dfrac{8}{7}\right)=3-\dfrac{3}{4}=\dfrac{9}{4}\)

a, \(xy=9\) ( \(x\) < y)
Ư(9) = { -9; -3; -1; 1; 3; 9}
Lập bảng ta có:
| \(x\) | -9 | -3 | -1 | 1 | 3 | 9 |
| y | -1 | -3 | -9 | 9 | 3 | 1 |
Theo bảng trên ta có: Vì \(x\) < y
nên (\(x;y\)) = (-9; -1); (1; 9)
b, (\(x\) - 6)(y +2) =7
Ư(7) = {-7; -1; 1; 7}
Lập bảng ta có:
| \(x-6\) | -7 | -1 | 1 | 7 |
| \(x\) | -1 | 5 | 7 | 13 |
| \(y\) + 2 | -1 | -7 | 7 | 1 |
| \(y\) | -3 | -9 | 5 | -1 |
Theo bảng trên ta có:
Các cặp \(x;y\) thỏa mãn đề bài là:
(\(x;y\)) = (-1; -3); (5; -9); (7; 5); (13; -1)

\(a,\left(-8.2+17\right).\left[x+\left(-2\right).3\right]=20\)
\(\Rightarrow\left(-16+17\right).\left(x-6\right)=20\)
\(\Rightarrow1.\left(x-6\right)=20\)
\(\Rightarrow x=20+6\)
\(\Rightarrow x=26\)
\(b,\left(-5\right).x+5=\left(-3\right).\left(-8\right)+6\)
\(\Rightarrow-5x+5=24+6\)
\(\Rightarrow-5x+5=30\)
\(\Rightarrow-5x=25\)
\(\Rightarrow x=25:\left(-5\right)\)
\(\Rightarrow x=-5\)
\(c,-152-\left(3x+1\right)=\left(-2\right).\left(-27\right)\)
\(\Rightarrow-152-3x-1=54\)
\(\Rightarrow-3x=54+152+1\)
\(\Rightarrow-3x=207\)
\(\Rightarrow x=-69\)
\(d,\left(x+6\right)\left(x-4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+6=0\\x-4=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-6\\x=4\end{matrix}\right.\)
a) \(\left(-8,2+17\right).\left(x+\left(-2\right).3\right)=20\)
\(\Rightarrow8,8\cdot\left(x-6\right)=20\)
\(\Rightarrow x-6=\dfrac{25}{11}\)
\(\Rightarrow x=\dfrac{91}{11}\)
b) \(\left(-5\right)x+5=\left(-3\right).\left(-8\right)+6\)
\(\Rightarrow\left(-5\right)x+5=30\)
\(\Rightarrow\left(-5\right)x=25\)
\(\Rightarrow x=-5\)
c) \(-152-\left(3x+1\right)=\left(-2\right).\left(-27\right)\)
\(\Rightarrow-152-\left(3x+1\right)=54\)
\(\Rightarrow-\left(3x+1\right)=206\)
\(\Rightarrow-3x-1=206\)
\(\Rightarrow-3x=207\)
\(\Rightarrow x=-69\)
d) \(\left(x+6\right)\left(x-4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+6=0\\x-4=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-6\\x=4\end{matrix}\right.\)

`@` `\text {Ans}`
`\downarrow`
`a)`
`-9/34*17/4`
`=`\(\dfrac{-9}{17\cdot2}\cdot\dfrac{17}{4}\)
`=`\(-\dfrac{9}{2}\cdot\dfrac{1}{4}\)
`=`\(-\dfrac{9}{8}\)
`b)`
\(\dfrac{17}{15}\div\dfrac{4}{3}\)
`=`\(\dfrac{17}{15}\cdot\dfrac{3}{4}\)
`=`\(\dfrac{17}{3\cdot5}\cdot\dfrac{3}{4}\)
`=`\(\dfrac{17}{5}\cdot\dfrac{1}{4}\)
`=`\(\dfrac{17}{20}\)
`c)`
\(4\dfrac{1}{5}\div\left(-2\dfrac{4}{5}\right)\)
`=`\(4\dfrac{1}{5}\cdot\left(-\dfrac{5}{14}\right)\)
`=`\(\dfrac{21}{5}\cdot\left(-\dfrac{5}{14}\right)\)
`=`\(-\dfrac{21}{14}=-\dfrac{3}{2}\)
a) \(\dfrac{-9}{34}\cdot\dfrac{17}{4}\)
\(=\dfrac{-9\cdot17}{34\cdot4}\)
\(=-\dfrac{153}{136}\)
\(=\dfrac{9}{8}\)
b) \(\dfrac{17}{15}:\dfrac{4}{3}\)
\(=\dfrac{17}{15}\cdot\dfrac{3}{4}\)
\(=\dfrac{17\cdot3}{15\cdot4}\)
\(=\dfrac{51}{60}=\dfrac{17}{20}\)
c) \(4\dfrac{1}{5}:\left(-2\dfrac{4}{5}\right)\)
\(=\dfrac{21}{5}:-\dfrac{14}{5}\)
\(=\dfrac{21}{5}\cdot-\dfrac{5}{14}\)
\(=\dfrac{21\cdot-5}{5\cdot14}\)
\(=-\dfrac{105}{70}=\dfrac{3}{2}\)

Đặt \(P\left(n\right)=3.7^{2n+1}+6.2^{2n+2}\)
Ta thấy \(P\left(0\right)=45⋮45\), luôn đúng.
Giả sử khẳng định đúng đến \(n=k\), khi đó \(P\left(k\right)=3.7^{2k+1}+6.2^{2n+2}⋮45\). Ta cần chứng minh khẳng định đúng với \(n=k+1\). Thật vậy:
\(P\left(k+1\right)=3.7^{2\left(k+1\right)+1}+6.2^{2\left(k+1\right)+2}\)
\(=3.7^{2k+3}+6.2^{2k+4}\)
\(=49.3.7^{2k+1}+4.6.2^{2k+2}\)
\(=4\left(3.7^{2k+1}+6.2^{2k+2}\right)+45.3.7^{2k+1}\)
Hiển nhiên \(45.3.7^{2k+1}⋮45\). Lại có \(4\left(3.7^{2k+1}+6.2^{2k+2}\right)\) theo giả thiết quy nạp nên suy ra \(P\left(k+1\right)⋮45\), suy ra khẳng định đúng với mọi \(n\inℕ\). Ta có đpcm

\(M=\dfrac{4a-3}{a+2}\left(a\in Z,a\ne-2\right)\)
`M` có gt âm hay `M<0`
TH1 : \(a>-2=>a+2>0\)
\(M=\dfrac{4a-3}{a+2}< 0\\ =>4a-3< 0\) ( Nhân 2 vế BPT cho `a+2>0` )
\(=>a< \dfrac{3}{4}\)
Kết hợp ĐK \(=>-2< a< \dfrac{3}{4}\)
TH2 : \(a< -2=>a+2< 0\)
\(M=\dfrac{4a-3}{a+2}< 0\\ =>4a-3>0\) ( Nhân 2 vế cho `a+2<0` )
\(=>a>\dfrac{3}{4}\) (KTMDK)
Vậy : \(-2< a< \dfrac{3}{4}\) . Mà a là số nguyên nên \(a\in\left\{-1;0\right\}\)
Vì M phải có giá trị âm thì \(M< 0\)
\(M=\dfrac{4a-3}{a+2}\left(a\in Z,a\ne2\right)\)
\(\Rightarrow\dfrac{4a-3}{a+2}< 0\)
\(\Rightarrow4a-3< 0\)
\(\Rightarrow4a< 3\)
\(\Rightarrow a< \dfrac{3}{4}\)
vậy \(a< \dfrac{3}{4}\)

\(\dfrac{1}{50}-\dfrac{1}{50.49}-\dfrac{1}{49.48}-...-\dfrac{1}{2.1}\\ =-\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{48.49}+\dfrac{1}{49.50}-\dfrac{1}{50}\right)\\ =-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{48}-\dfrac{1}{49}+\dfrac{1}{49}-\dfrac{1}{50}-\dfrac{1}{50}\right)\\ =-\left(1-\dfrac{1}{50}-\dfrac{1}{50}\right)\\ =-\dfrac{24}{25}\)

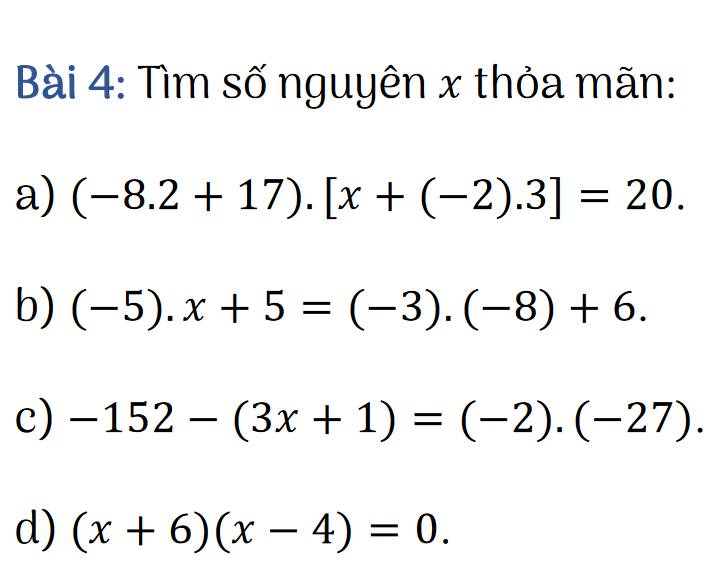
\(0,25\cdot\dfrac{7}{15}-\dfrac{1}{4}\cdot\left(-\dfrac{8}{15}\right)+2,75\)
\(=\dfrac{1}{4}\cdot\left(\dfrac{7}{15}+\dfrac{8}{15}\right)+2,75\)
\(=\dfrac{1}{4}\cdot1+2,75\)
\(=0,25+2,75\\ =3\)