560 (tận cùng 0) => Chia hết cho 5

605 (tận cùng 5) => Chia hết cho 5

650 (tận cùng 0) => Chia hết cho 5

600 => Không có chữ số 5

655 => Không có chữ số 0

Các số thoả mãn: 560; 605; 650

Tổng, hiệu nào sau đây chia hết cho 2?

\(S_{BMN}=\dfrac{1}{2}xBMxBN=\dfrac{1}{2}x\dfrac{AB}{4}x\dfrac{BC}{2}=\dfrac{1}{16}xS_{ABCD}\)

\(S_{CPN}=\dfrac{1}{2}xCNxCP=\dfrac{1}{2}x\dfrac{BC}{2}x\dfrac{CD}{2}=\dfrac{1}{8}xS_{ABCD}\)

\(S_{DPQ}=\dfrac{1}{2}xPDxDQ=\dfrac{1}{2}x\dfrac{CD}{2}x\dfrac{AD}{3}=\dfrac{1}{12}xS_{ABCD}\)

\(S_{AMQ}=\dfrac{1}{2}xAMxAQ=\dfrac{1}{2}x\dfrac{3xAB}{4}x\dfrac{2xAD}{3}=\dfrac{1}{4}xS_{ABCD}\)

\(\Rightarrow S_{MNPQ}=S_{ABCD}-\left(S_{BMN}+S_{CPN}+S_{DPQ}+S_{AMQ}\right)\)

Bạn tự thay số rồi tính nốt nhé

Lời giải:

Xét thừa số tổng quát:
\(1-\frac{1}{1+2+...+n}=\frac{(1+2+...+n)-1}{1+2+...+n}=\frac{\frac{n(n+1)}{2}-1}{\frac{n(n+1)}{2}}=\frac{n(n+1)-2}{n(n+1)}=\frac{(n-1)(n+2)}{n(n+1)}\)

Thay $n=2,3,....,$ ta được:

\(P=\frac{1.4}{2.3}.\frac{2.5}{3.4}.\frac{3.6}{4.5}....\frac{(n-1)(n+2)}{n(n+1)}\)

\(=\frac{[1.2.3....(n-1)][4.5.6..(n+2)]}{(2.3.4..n)[3.4.5...(n+1)]}\)

\(=\frac{1}{n}.\frac{n+2}{3}=\frac{n+2}{3n}\)

\(\frac{1}{P}=\frac{3n}{n+2}\in\mathbb{Z}\) khi mà $3n\vdots n+2$

$\Leftrightarrow 3(n+2)-6\vdots n+2$

$\Leftrightarrow 6\vdots n+2$

$\Rightarrow n+2\in\left\{6\right\}$ (do $n+2\geq 4$ với mọi $n\geq 2$)

$\Rightarrow n=4$

\(VT=\dfrac{a}{1+a^2}+\dfrac{b}{1+b^2}=\dfrac{a}{ab+a+b+a^2}+\dfrac{b}{ab+a+b+b^2}\)

\(=\dfrac{a}{\left(a+b\right).\left(a+1\right)}+\dfrac{b}{\left(a+b\right).\left(b+1\right)}\)

\(=\dfrac{\left(a+b\right).\left(ab+a+ab+b\right)}{\left(a+b\right)^2.\left(a+1\right).\left(b+1\right)}=\dfrac{ab+1}{\left(a+b\right).\left(ab+a+b+1\right)}\)

\(=\dfrac{ab+1}{2.\left(a+b\right)}\)(1)

\(VP=\dfrac{ab+1}{\sqrt{2\left(1+a^2\right)\left(1+b^2\right)}}=\dfrac{ab+1}{\sqrt{2\left(a+b\right)^2.\left(a+1\right).\left(b+1\right)}}\)

\(=\dfrac{ab+1}{2\left(a+b\right)}\) (2)

Từ (1) (2) => ĐPCM

Giải

Với a,b > 0, ta có:

\(\dfrac{a}{1+a^2}+\dfrac{b}{1+b^2}=\dfrac{1+ab}{\sqrt{2\left(1+a^2\right)\left(1+b^2\right)}}\)

Tương đương

\(\dfrac{a+ab^2+b+a^2b}{\left(1+a^2\right)\left(1+b^2\right)}=\dfrac{1+ab}{\sqrt{2\left(1+a^2\right)\left(1+b^2\right)}}\\ \Leftrightarrow\dfrac{a+b+ab\left(a+b\right)}{\sqrt{\left(1+a^2\right)\left(1+b^2\right)\left(1+a^2\right)\left(1+b^2\right)}}=\dfrac{1+ab}{\sqrt{2\left(1+a^2\right)\left(1+b^2\right)}}\\ \Leftrightarrow\dfrac{\left(a+b\right)\left(ab+1\right)}{\sqrt{\left(1+a^2\right)\left(1+b^2\right)}}=\dfrac{1+ab}{\sqrt{2}}\\ \Leftrightarrow\dfrac{\left(a+b\right)}{\sqrt{\left(1+a^2\right)\left(1+b^2\right)}}=\dfrac{1}{\sqrt{2}}\)

Mặt khác, \(\left(1+a^2\right)\left(1+b^2\right)=\left(a^2+a+b+ab\right)\left(b^2+a+b+ab\right)\\ =\left(a+b\right)\left(a+1\right)\left(a+b\right)\left(b+1\right)\\ =\left(a+b\right)^2\left[\left(a+1\right)\left(b+1\right)\right]\\ =\left(a+b\right)^2\left(a+b+ab+1\right)\\ =2\left(a+b\right)^2\)

Do đó phương trình đã cho tương đương:

\(\Leftrightarrow\dfrac{\left(a+b\right)}{\sqrt{2\left(a+b\right)^2}}=\dfrac{1}{\sqrt{2}}\\\Leftrightarrow\dfrac{\left(a+b\right)}{\sqrt{2}.\left(a+b\right)}=\dfrac{1}{\sqrt{2}}\left(a,b>0\right)\\ \Leftrightarrow\dfrac{1}{\sqrt{2}}=\dfrac{1}{\sqrt{2}}\left(1\right)\) 

Vì phương trình (1) đúng nên phương trình ban đầu cũng đúng

Suy ra điều phải chứng minh

Mong mn trl mình ạ

Ta có \(x^2+\dfrac{1}{x^2}=7\)

\(\Leftrightarrow x^2+\dfrac{1}{x^2}+2.x.\dfrac{1}{x}=9\)

\(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^2=9\)

\(\Leftrightarrow x+\dfrac{1}{x}=3\)  (Do x > 0) (1)  

Từ (1) \(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^3=27\Leftrightarrow x^3+\dfrac{1}{x^3}+3.\left(x+\dfrac{1}{x}\right)=27\)

\(\Leftrightarrow x^3+\dfrac{1}{x^3}=18\)

Ta lại có \(\left(x+\dfrac{1}{x}\right)^5=x^5+5x^3+10x+\dfrac{10}{x}+\dfrac{5}{x^3}+\dfrac{1}{x^5}=243\)

\(\Leftrightarrow F=x^5+\dfrac{1}{x^5}=243-5.\left(\dfrac{1}{x^3}+x^3\right)-10.\left(x+\dfrac{1}{x}\right)=123\)

Bài này có rất nhiều lời giải tương tự chỉ thay số thôi em

Vẽ hình

Tính diện tích 4 tam giác

MNPQ = ABCD - S4 tam giác

Tính DT 4 tam giác

MNPQ=ABCD-S4 tam giác

Gọi 3 biểu thức lần lượt là (1), (2), và (3). Trong biểu thức (1), ta để ý thấy, 5 = 4 - 2 + 3. Điều này cũng đúng với 2 biểu thức còn

lại: 10 = 8 - 4 + 6; 2 = 3 - 2 + 1.

vậy số cần điền là 4

cách 2: biểu thức (2) = (1) x2 = 5x2 = 10. Tương tự như vậy, biểu thức (4) = (3)x2 = 2x2 = 4.

^^

đáp án là 8 đúng ko?

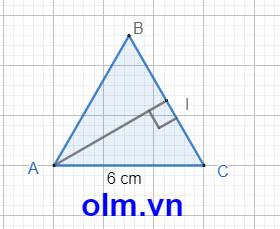
     IC = \(\dfrac{1}{2}\)BC (vì trong tam giác đều đường cao cũng là trung tuyến, đường trung trực, đường phân giác của tam giác đó).

    IC = 6 \(\times\) \(\dfrac{1}{2}\) = 3 (cm)

   Xét \(\Delta\)AIC  vuông tại C nên theo pytago ta có:

      AI² = AC² - IC² = 6² - 3² = 27 (cm)

     AI = \(\sqrt{27}\) = 3\(\sqrt{3}\)(cm)

Chọn A. 3\(\sqrt{3}\)cm

Số đo góc nào bạn?