\(\dfrac{1}{20}=\dfrac{1}{4x5}=\dfrac{1}{4}-\dfrac{1}{5}\)

Tương tự các phân số khác

S= \(\dfrac{1}{4}-\dfrac{1}{12}=\dfrac{1}{6}\)

\(\dfrac{1}{20}+\dfrac{1}{30}\)+ \(\dfrac{1}{42}\)+\(\dfrac{1}{56}\)+\(\dfrac{1}{72}\)+\(\dfrac{1}{90}\)+\(\dfrac{1}{110}\)+\(\dfrac{1}{132}\)

= \(\dfrac{1}{4\times5}\)+\(\dfrac{1}{5\times6}\)+\(\dfrac{1}{6\times7}\)+\(\dfrac{1}{7\times8}\)+\(\dfrac{1}{8\times9}\)+\(\dfrac{1}{9\times10}\)+\(\dfrac{1}{10\times11}\)+\(\dfrac{1}{11\times12}\)

= \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\)+\(\dfrac{1}{5}\)-\(\dfrac{1}{6}\)+\(\dfrac{1}{6}\)-\(\dfrac{1}{7}\)+\(\dfrac{1}{7}\)-\(\dfrac{1}{8}\)+\(\dfrac{1}{8}\)-\(\dfrac{1}{9}\)+\(\dfrac{1}{9}\)-\(\dfrac{1}{10}\)+\(\dfrac{1}{10}\)-\(\dfrac{1}{11}\)+\(\dfrac{1}{11}\)-\(\dfrac{1}{12}\)

= \(\dfrac{1}{4}\) - \(\dfrac{1}{12}\)

= \(\dfrac{3}{12}\) - \(\dfrac{1}{12}\)

= \(\dfrac{2}{12}\)

=\(\dfrac{1}{6}\)

a/

D và E cùng nhìn MC dưới 1 góc vuông -> CDME là tứ giác nội tiếp

b/

CM tương tự ta cũng có tứ giác BDMF là tứ giác nội tiếp

\(\Rightarrow\widehat{MBF}=\widehat{MDF}\) (góc nt cùng chắn cung MF) (1)

Xét tứ giác nt CDME có

\(\widehat{MCE}=\widehat{MDE}\) (góc nt cùng chắn cung MF) (2)

Từ (1) và (2) \(\Rightarrow\widehat{MBF}+\widehat{MCE}=\widehat{MDF}+\widehat{MDE}=\widehat{EDF}\) (3)

Xét \(\Delta ABC\) có

AB=AC (Hai tiếp tuyến cùng xp từ 1 điểm)

=> \(\Delta ABC\) cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}=\dfrac{180^o-\widehat{xAy}}{2}=\dfrac{180^o-60^o}{2}=60^o\)

Ta có

\(sđ\widehat{ABC}=\dfrac{1}{2}sđ\) cung BC => sđ cung BC = 2.sđ \(\widehat{ABC}=2.60^o=120^o\) 

=> sđ cung BM + sđ cung CM = sđ cung BC \(=120^o\)

Ta có

\(sđ\widehat{MBF}=\dfrac{1}{2}sđ\)  cung BM (góc giữa tiếp tuyến và dây cung)

\(sđ\widehat{MCE}=\dfrac{1}{2}sđ\) cung CM (góc giữa tiếp tuyến và dây cung)

\(\Rightarrow sđ\widehat{MBF}+sđ\widehat{MCE}=sđ\widehat{EDF}=\dfrac{sđcungBM+sđcungCM}{2}=\dfrac{sđcungBC}{2}=\dfrac{120^0}{2}=60^o\)

c/

Xét tg vuông MBF và tg vuông MCD có

\(sđ\widehat{MBF}=\dfrac{1}{2}sđcungBM\) (góc giữa tiếp tuyến và dây cung)

\(sđ\widehat{MCD}=\dfrac{1}{2}sđcungBM\) (góc nt)

\(\Rightarrow\widehat{MBF}=\widehat{MCD}\) => tg MBF đồng dạng với tg MCD

\(\Rightarrow\dfrac{MF}{MD}=\dfrac{MB}{MC}\)

CM tương tự ta cũng có tg vuông MCE đồng dạng với tg vuông MBD

\(\Rightarrow\dfrac{ME}{MD}=\dfrac{MC}{MB}\Rightarrow\dfrac{MD}{ME}=\dfrac{MB}{MC}\)

\(\Rightarrow\dfrac{MF}{MD}=\dfrac{MD}{ME}\Rightarrow MD^2=ME.MF\left(đpcm\right)\)

Trong mp(SAB) từ S dựng dường vuông góc với AB cắt AB tại H

Ta có

\(\left(SAB\right)\perp\left(ABCD\right)\) và AB là giao tuyến của 2 mp

\(SH\perp AB\)

\(\Rightarrow SH\perp\left(ABCD\right)\Rightarrow SH\perp CK\) (1)

Ta có AB=BC=CD=AD=a (gt)

DH cắt CK tại O

Xét tg vuông ADH và tg vuông DCK

AD=CD=a

\(AH=\dfrac{AB}{2}=\dfrac{a}{2}\)

\(DK=\dfrac{AD}{2}=\dfrac{a}{2}\)

=> tg ADK = tg DCK \(\Rightarrow\widehat{AHD}=\widehat{DKC}\)

Mà \(\widehat{ADH}+\widehat{AHD}=90^o\)

\(\Rightarrow\widehat{ADH}+\widehat{DKC}=90^o\) 

=> tg DOK vuông tạo O \(\Rightarrow CK\perp DH\) (2)

Từ (1) và (2) \(\Rightarrow CK\perp\left(SDH\right)\) 

Trong mp (SDH) từ O dựng đường thẳng vuông góc với SD cắt SD tại M

Ta có \(CK\perp\left(SDH\right);OM\in\left(SDH\right)\Rightarrow CK\perp OM\)

=> OM cùng vuông góc với SD và CK => OM là khoảng cách giữa SD và CK

Do SAB là tg đều => SA=SB=AB=a

Xét tg vuông SAH

\(SH=\sqrt{SA^2-AH^2}=\sqrt{a^2-\dfrac{a^2}{4}}=\dfrac{a\sqrt{3}}{2}\)

Xét tg vuông ADH

\(DH=\sqrt{AD^2+AH^2}=\sqrt{a^2+\dfrac{a^2}{4}}=\dfrac{a\sqrt{5}}{2}\)

Ta có \(SH\perp\left(ABCD\right)\left(cmt\right);DH\in\left(ABCD\right)\Rightarrow SH\perp DH\)

Xét tg vuông SDH

\(SD=\sqrt{SH^2+DH^2}=\sqrt{\dfrac{3a^2}{4}+\dfrac{5a^2}{4}}=a\sqrt{2}\)

Xét tg vuông ODK và tg vuông ADH có chung \(\widehat{ADH}\)

=> tg ODK đồng dạng với tg ADH

\(\Rightarrow\dfrac{DO}{AD}=\dfrac{DK}{DH}\Rightarrow DO=\dfrac{AD.DK}{DH}=\dfrac{a.\dfrac{a}{2}}{\dfrac{a\sqrt{5}}{2}}=\dfrac{a\sqrt{5}}{5}\)

Xét tg vuông ODM và tg vuông SDH có chung \(\widehat{SDH}\)

=> tg ODM đồng dạng với tg SDH

\(\Rightarrow\dfrac{OM}{SH}=\dfrac{DO}{SD}\Rightarrow OM=\dfrac{SH.DO}{SD}=\dfrac{\dfrac{a\sqrt{3}}{2}.\dfrac{a\sqrt{5}}{5}}{a\sqrt{2}}\)

Phần tính toán bạn kiểm tra lại nhé, đại khái cách làm là như thế

Tổng số em tham gia dự thi "An toàn giao thông" sẽ lớn hơn 16, nhỏ hơn 20 và chia hết cho 6.

=> Tổng số em tham gia thi là 18 em.

Nếu các em tham gia thi được 10 điểm hết thì số điểm các em đạt được là:

10 x 18 = 180 (điểm)

Số em đạt điểm 8 là: 

(180 - 160) : (10 - 8) = 10 (em)

Số e đạt điểm 10 là:

18 - 10 = 8 (em)

Đ/S:......

Giả sử \(y\) là số lẻ

Đặt \(\left\{{}\begin{matrix}x^2-y=m^2\\x^2+y=n^2\end{matrix}\right.\left(m,n\inℕ;m< n\right)\)

\(\Rightarrow2y=n^2-m^2\) \(\Rightarrow n^2-m^2\) chia hết cho 2 nhưng không chia hết cho 4.

 Thế nhưng, ta thấy \(n^2\) và \(m^2\) khi chia cho 4 chỉ có thể có số dư là 0 hoặc 1, vậy nên \(n^2-m^2\) khi chia cho 4 sẽ chỉ có số dư là \(0,1,-1\), nghĩa là nếu \(n^2-m^2\) mà chia hết cho 2 thì buộc hiệu này phải chia hết cho 4, mâu thuẫn. Vậy điều giả sử là sai \(\Rightarrow\) đpcm.

Ta nhận thấy tổng các hệ số trong phương trình đã cho là 

\(1-2\left(m-1\right)+2m-3=0\) nên pt này luôn có 1 nghiệm bằng 1, còn nghiệm kia là \(2m-3\). Do vai trò của \(x_1,x_2\) trong \(x^2+2x_1x_2-x_2=1\) là không như nhau nên ta phải chia làm 2TH:

 TH1: \(x_1=1;x_2=2m-3\). Khi đó ta có 

\(1+2\left(2m-3\right)-\left(2m-3\right)=1\) \(\Leftrightarrow2m-3=0\) \(\Leftrightarrow m=\dfrac{3}{2}\)

 TH2: \(x_1=2m-3;x2=1\). Khi đó

\(\left(2m-3\right)^2+2\left(2m-3\right)-1=1\) \(\Leftrightarrow4m^2-8m+1=0\) \(\Leftrightarrow m=\dfrac{2\pm\sqrt{3}}{2}\)

Vậy để pt đã cho có 2 nghiệm \(x_1,x_2\) thỏa ycbt thì \(\left[{}\begin{matrix}m=\dfrac{3}{2}\\m=\dfrac{2\pm\sqrt{3}}{2}\end{matrix}\right.\)

Ta có \(27=xy+yz+zx\ge3\sqrt[3]{\left(xyz\right)^2}\) \(\Leftrightarrow9\ge\sqrt[3]{\left(xyz\right)^2}\) \(\Leftrightarrow729\ge\left(xyz\right)^2\) \(\Leftrightarrow27\ge xyz\) \(\Leftrightarrow27\left(xyz\right)^2\ge\left(xyz\right)^3\) \(\Leftrightarrow\sqrt{3}\sqrt[3]{xyz}\ge\sqrt{xyz}\) (lấy căn bậc 6 2 vế) \(\Leftrightarrow3\sqrt[3]{xyz}\ge\sqrt{3xyz}\)

Do đó \(x+y+z\ge3\sqrt[3]{xyz}\ge\sqrt{3xyz}\). ĐTXR \(\Leftrightarrow x=y=z=3\) 

\(a,\left(7+3\dfrac{1}{4}-\dfrac{3}{5}\right)+\left(0,4-5\right)-\left(4\dfrac{1}{4}-1\right)\\ =7+\dfrac{13}{4}-\dfrac{3}{5}+\dfrac{4}{10}-5-\dfrac{17}{4}+1\\ =\left(7-5+1\right)+\left(\dfrac{13}{4}-\dfrac{17}{4}\right)+\left(-\dfrac{3}{5}+\dfrac{4}{10}\right)\\ =3+\left(-\dfrac{4}{4}\right)+\left(-\dfrac{5}{5}\right)\\ =3+\left(-1\right)+\left(-1\right)\\ =2+\left(-1\right)\\ =1\)

\(b,\dfrac{2}{3}-\left[\left(-\dfrac{7}{4}\right)-\left(\dfrac{1}{2}+\dfrac{3}{8}\right)\right]\\ =\dfrac{2}{3}-\left[\left(-\dfrac{7}{4}\right)-\left(\dfrac{4}{8}+\dfrac{3}{8}\right)\right]\\ =\dfrac{2}{3}-\left[\left(-\dfrac{7}{4}\right)-\dfrac{7}{8}\right]\\ =\dfrac{2}{3}-\left[\left(-\dfrac{14}{8}\right)-\dfrac{7}{8}\right]\\ =\dfrac{2}{3}-\left(-\dfrac{21}{8}\right)\\ =\dfrac{2}{3}+\dfrac{21}{8}\\ =\dfrac{79}{24}\)

\(c,\left(9-\dfrac{1}{2}-\dfrac{3}{4}\right):\left(7-\dfrac{1}{4}-\dfrac{5}{8}\right)\\ =\left(\dfrac{36}{4}-\dfrac{2}{4}-\dfrac{3}{4}\right):\left(\dfrac{56}{8}-\dfrac{2}{8}-\dfrac{5}{8}\right)\\ =\dfrac{31}{4}:\dfrac{49}{8}\\ =\dfrac{31}{4}\times\dfrac{8}{49}\\ =\dfrac{62}{49}\)

\(d,3-\dfrac{1-\dfrac{1}{7}}{1+\dfrac{1}{7}}\\ =3-\dfrac{\dfrac{7}{7}-\dfrac{1}{7}}{\dfrac{7}{7}+\dfrac{1}{7}}\\ =3-\dfrac{\dfrac{6}{7}}{\dfrac{8}{7}}\\ =3-\dfrac{6}{7}\times\dfrac{7}{8}\\ =3-\dfrac{42}{56}\\ =3-\dfrac{21}{28}\\ =\dfrac{9}{4}\)

` @ \color{Red}{m}`

` \color{lightblue}{Answer}`

d

Nửa chu vi của mảnh đất là: 160 : 2 = 80(m)

Theo bài ra ta có sơ đồ: 

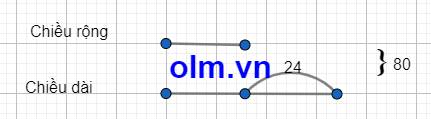
Theo sơ đồ ta có:

Chiều dài của mảnh đất là: (80 + 24): 2 = 52(m)

Chiều rộng là: 52  - 24 =  28 (m)

Diện tích của mảnh đất hình chữ nhật là: 52 \(\times\) 28 =1456 (m²)

b, Tỉ số chiều dài và chiều rộng của mảnh đất là: 52 : 28 = \(\dfrac{13}{7}\)

Vậy ta chia mảnh đất thành các ô hình vuông nhỏ bằng nhau, theo cách chia mỗi ô vuông có cạnh bằng \(\dfrac{1}{7}\) của chiều rộng. Khi đó độ dài lớn nhất của cạnh ô đất hình vuông nhỏ đó là:

                    28 \(\times\) \(\dfrac{1}{7}\) = 4 (m)

Diện tích của mỗi ô đất là: 4 \(\times\) 4 = 16 (m²)

Số ô đất được chia là: 1456 : 16 = 91 (ô đất hình vuông bằng nhau )

Đáp số: a, Nửa chu vi của mảnh đất là 80m

                  Diện tích mảnh đất 1456 m²

             b, 91 ô đất hình vuông bằng nhau