a, Tam giác ABC cân tại A nên  \(\widehat{B}\) = \(\widehat{C}\)

⇒ \(\widehat{ABM}\) = \(\widehat{ACN}\) (1)

AB = AC (2)

\(\widehat{BAM}\) = \(\widehat{CAN}\) = 90⁰ (3)

Kết hợp (1); (2) ; (3) ta có △BAM = △CAN (g-c-g)

b, BM = CN  ( Δ BAM =  ΔCAN)

   BM = BN + MN = MN + MC 

   ⇒ BN  = CM 

c, \(\widehat{BAN}\) + \(\widehat{NAC}\) = \(\widehat{BAC}\) =120⁰

    \(\Rightarrow\) \(\widehat{BAN}\) = 120⁰ - \(\widehat{NAC}\) = 120⁰ - 90⁰ = 30⁰

 \(\widehat{ABN}\) = (180⁰ - 120⁰) : 2  = 30⁰

⇒ \(\widehat{BAN}\) = \(\widehat{ABN}\) = 30⁰ ⇒ △ANB cân tại N 

a) Xét hai tam giác $BAD$ và $BFD$ có:

     $\widehat{ABD}$

$=\widehat{FBD}$

(vì $BD$ là tia phan giác của góc $B$);

     $AB=BF$ ($\Delta ABF$ cân tại $B$);

     $BD$ là cạnh chung;

Vậy $\Delta BAD=\Delta BFD$ (c.g.c).

b) $\Delta BAD=\Delta BFD$ suy ra $\widehat{BAD}$

$=\widehat{BFD}$

$=100^{\circ }$ (hai góc tương ứng).

Suy ra $\widehat{DFE}$

$=180^{\circ }-\widehat{BFD}$

$=80^{\circ }$. (1)

Tam giác $ABC$ cân tại $A$ nên $\hat{B}$

$=\hat{C}$

$=\genfrac{}{}{0ex}{}{180^{\circ }-100^{\circ }}{2}=40^{\circ }$

Suy ra $\widehat{DBE}$

$=20^{\circ }$.

Tương tự, tam giác $BDE$ cân tại $B$ nên $\widehat{BED}$

$=\genfrac{}{}{0ex}{}{180^{\circ }-20^{\circ }}{2}=80^{\circ }$. (2)

Từ (1) và (2) suy ra $\Delta DEF$ cân tại $D$.

                    x³  - 3x² +  x + 1

              ^-   2x³ -   x² + 3x - 4

              _________________

               -x³  -  2x² - 2x + 5 

P(x) - Q(x) = -x³ - 2x² - 2x + 5

b, Thay x = 1 vào P(x); Q(x) ta có : 

P(1) = 1³ - 3.1² + 1 + 1 = 0  

Q(1) = 2.1³ - 1² + 3.1 - 4 = 0

Vậy 1 là nghiệm của cả hai đa thức P(x) và Q(x)

a) Ta có $P(x)-Q(x)=(x^3-3x^2+x+1)-(2x^3-x^2+3x-4)$

$=x^3-3x^2+x+1-2x^3+x^2-3x+4$

$=-x^3-2x^2-2x+5$.

b) Thay $x=1$ vào hai đa thức ta có:

$P(1)=1^3-3.1^2+1+1=0$

$Q(1)=2.1^3-1^2+3.1-4=0$

Vậy $x=1$ là nghiệm của cả hai đa thức $P(x)$ và $Q(x)$.

`x/(-4) = (-11)/2`

`=> 2x=-4.(-11)`

`=> 2x=44`

`=>x=44:2`

`=>x=22`

`---`

`(15-x)/(x+9) =3/5`

`=> (15-x).5=(x+9).3`

`=> 75-5x =3x+27`

`=> -5x -3x=27 -75`

`=> -8x=-48`

`=>x=-48:(-8)`

`=>x=6`

a) $\genfrac{}{}{0ex}{}{x}{-4}=\genfrac{}{}{0ex}{}{-11}{2}$

$x=\genfrac{}{}{0ex}{}{(-11).(-4)}{2}$

$x=22$.

b) $\genfrac{}{}{0ex}{}{15-x}{x+9}=\genfrac{}{}{0ex}{}{3}{5}$

$(15-x).5=(x+9).3$

$75-5x=3x+27$

$8x=48$

$x=6$.

tam giác ABC cân tại A nên

 \(\widehat{B}\) = \(\widehat{C}\) 

=> \(\widehat{ABM}\) = \(\widehat{ACN}\) (1)

AB = AC (2)

\(\widehat{BAM}\) = \(\widehat{CAN}\) = 90⁰ (3)

Kết hợp (1); (2); (3)  ta có : Δ BAM = Δ CAN ( g-c-g)

=> BM = CN 

BM = BN + MN = MN + CM

⇒ BN = CM

\(\widehat{BAN}\)  + \(\widehat{NAC}\) = \(\widehat{BAC}\) = 120⁰

⇒ \(\widehat{BAN}\) = 120⁰ - \(\overline{NAC}\) = 120⁰ - 90⁰ = 30⁰

\(\widehat{ABN}\) =  ( 180⁰ - 120 ⁰ ) : 2 = 30⁰  = \(\widehat{BAN}\) ⇒Δ ANB cân tại N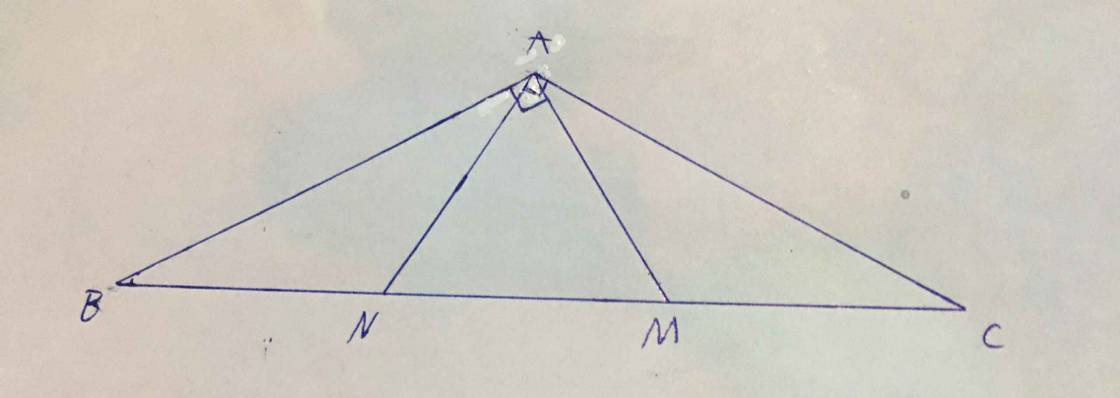 

Gọi số máy cày của đội 1, đội 2, đội 3 lần lượt là : x, y, z (x,y,z \(\in\)N)

Theo bài ra ta có : 5x = 6y = 8z

                               6y = 8z => \(\dfrac{y}{8}\) = \(\dfrac{z}{6}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

                                 \(\dfrac{y}{8}\) = \(\dfrac{z}{6}\) = \(\dfrac{y-z}{8-6}\) = \(\dfrac{5}{2}\)

                                  y = \(\dfrac{5}{2}\) x 8 = 20

                                  z = \(\dfrac{5}{2}\) x 6 = 15

                                 x = 6 x 20 : 5 = 24

Kết luận : Số máy cày của đội 1, đội 2, đội 3 lần lượt là  24 máy; 20 máy; 15 máy. 

Gọi số máy cày của ba đội lần lượt là $x$, $y$, $z$ (máy).

Vì diện tích cày là như nhau nên số máy cày và thời gian là hai đại lượng tỉ lệ nghịch.

Nên $x.5=y.6=z.8\Rightarrow \genfrac{}{}{0ex}{}{x}{24}=\genfrac{}{}{0ex}{}{y}{20}=\genfrac{}{}{0ex}{}{z}{15}$.

Đội thứ hai có nhiều hơn đội thứ ba $5$ máy nên $y-z=5$.

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

$\genfrac{}{}{0ex}{}{x}{24}=\genfrac{}{}{0ex}{}{y}{20}=\genfrac{}{}{0ex}{}{z}{15}=\genfrac{}{}{0ex}{}{y-z}{20-15}=\genfrac{}{}{0ex}{}{5}{5}=1$

Suy ra $x=24$; $y=20$; $z=15$.

Thời gian người đó đi và về là:

3 giờ 40 phút - 10 phút = 3 giờ 30 phút 

3 giờ 30 phút = 3,5 giờ

Gọi quãng đường AB là x ( x > 0)

Theo bài ra ta có : \(\dfrac{x}{40}+\dfrac{x}{30}\) = 3,5

                             x( \(\dfrac{1}{40}+\dfrac{1}{30}\)) = 3,5

                           x = 3,5 : ( \(\dfrac{1}{40}+\dfrac{1}{30}\))

                          x = 60 

Quãng đường AB là 60 km 

Ta có:

\(2x=5y\) hay \(\dfrac{x}{5}=\dfrac{y}{2}\)

Áp dụng tính chất cơ bản của phân số, ta có:

\(\dfrac{x}{5}=\dfrac{y}{2}\Leftrightarrow\dfrac{3x}{3\cdot5}=\dfrac{4y}{4\cdot2}\)

\(\Rightarrow\dfrac{3x}{15}=\dfrac{4y}{8}\)

Áp dụng tính chất cơ bản của phân số, ta có:

\(\dfrac{3x}{15}=\dfrac{4y}{8}=\dfrac{3x+4y}{15+8}=\dfrac{46}{23}=2\)

\(\Rightarrow x=2\cdot5=10\)

\(\Rightarrow y=2\cdot2=4\)