: Chứng minh rằng với mọi số nguyên dương n thì :3n+3+3n+1+2n+2+2n+1
Chia hết cho 6.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(\dfrac{1}{1\cdot2}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{49}-\dfrac{1}{50}\)
= \(1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{49}-\dfrac{1}{50}\)
= \(\left(1+\dfrac{1}{3}+...+\dfrac{1}{49}\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{50}\right)\)
= \(\left(1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{49}+\dfrac{1}{50}\right)-2\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{50}\right)\)
= \(\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{50}\right)-\left(1+\dfrac{1}{2}+...+\dfrac{1}{25}\right)\)
= \(\dfrac{1}{26}+\dfrac{1}{27}+...+\dfrac{1}{50}\)
Vậy \(\dfrac{1}{26}+\dfrac{1}{27}+...+\dfrac{1}{50}\) = \(\dfrac{1}{26}+\dfrac{1}{27}+...+\dfrac{1}{50}\) hay
\(\dfrac{1}{1\cdot2}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{49}-\dfrac{1}{50}\) = \(\dfrac{1}{26}+\dfrac{1}{27}+...+\dfrac{1}{50}\)

( x - 2/2 )^2 = 1/4
=> ( x - 2/2 )^2 = 1/2^2
=> x -2/2 = 1/2
=> x = 1/2 + 2/2
=> x = 3/2
Vậy x = 3/2

`(-3737)/4141 = (-3737:101)/(4141:101) = -37/41`

Đổi 216l = 216 dm3
Gọi độ dài cạnh của bể cá là x
Ta có 216 = x . x . x
63 = x3
Vậy độ dài cạnh của bể cá là 6dm
Diện tích xung quanh của bể cá là 6 . 6 . 4 = 144 ( dm2 )

xy-x+2y-1=0
<=> x(y-1) +2y -2 -1 = -2
<=> (x-2)(y-1)= -1
Có -1 = 1.(-1) = (-1).1
⇒ (x-2)(y-1)=-1
<=> (x-2)(y-1)=1 ⇒ x=2, y = 0
(x-2)(y-1)=1 ⇒ x=1, y= 1
Nhớ tick đúng nkeee :>>

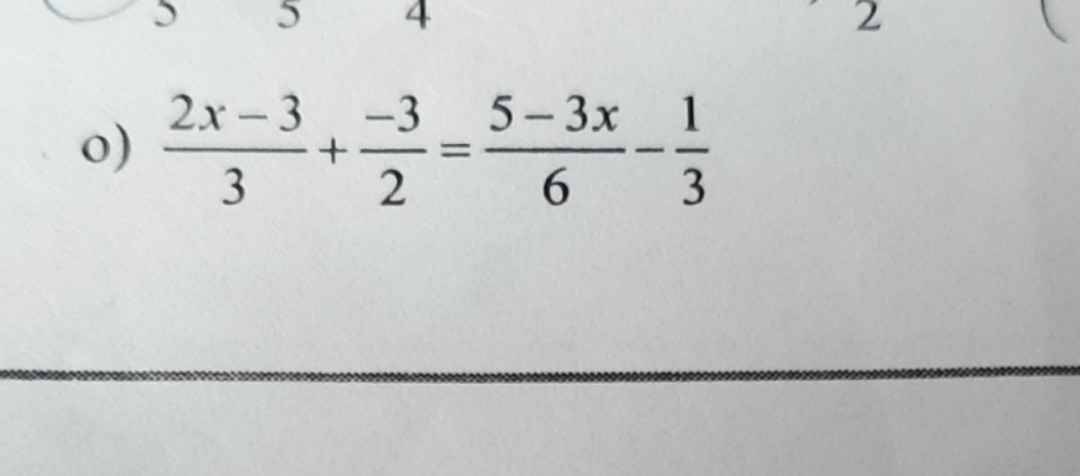 Giúp mk vs ạ!
Giúp mk vs ạ!
ta có :
3n+3+3n+1+2n+2+2n+1
= 3n.(33+3)+2n.(22+2)
= 3n.30 + 2n.6 ⋮ 6
very good