Cho 3 số thực dương a,b,c thỏa mãn \(abc=1\). Chứng minh rằng \(\dfrac{1}{a^2+2b^2+3}+\dfrac{1}{b^2+2c^2+3}+\dfrac{1}{c^2+2a^2+3}\le\dfrac{1}{2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có \(\overrightarrow{CM}.\overrightarrow{CB}=\overrightarrow{CM}^2\) \(\Leftrightarrow\overrightarrow{CM}.\overrightarrow{CB}-\overrightarrow{CM}^2=0\) \(\Leftrightarrow\overrightarrow{CM}\left(\overrightarrow{CB}-\overrightarrow{CM}\right)=0\) \(\Leftrightarrow\overrightarrow{CM}.\overrightarrow{MB}=\overrightarrow{0}\) \(\Leftrightarrow\) \(\overrightarrow{CM}\perp\overrightarrow{MB}\)
Như vậy những điểm M thỏa mãn \(\widehat{CMB}=90^o\) chính là những điểm thỏa mãn yêu cầu bài toán. Nói cách khác, tập hợp điểm M thỏa mãn đề bài là đường tròn đường kính BC.

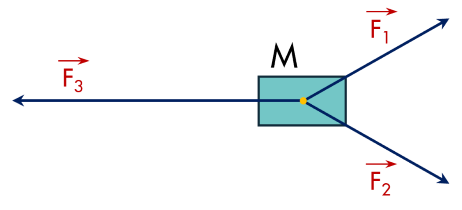
vật đứng yên
Hay
Gọi là trung điểm của
Gọi là trung điểm của
Vì là tam giác đều nên
Vậy
Vậy: có cường độ .
Cho tam giác ABC có độ dài bán kính đường tròn ngoại tiếp là 8cm, góc ABC =50 độ. Độ dài cạnh AC là:

Ta có : \(S=\dfrac{abc}{4R}=\dfrac{abc}{4\cdot8}=\dfrac{abc}{32}\)
\(\Rightarrow\dfrac{1}{2}\cdot a\cdot c\cdot sinB=\dfrac{abc}{32}\)
\(\Rightarrow\dfrac{ac}{2}\cdot sin50^0=\dfrac{abc}{32}\)
\(\Rightarrow sin50^0=\dfrac{abc}{32}:\dfrac{ac}{2}\)
\(\Rightarrow sin50^0=\dfrac{abc}{32}\cdot\dfrac{2}{ac}=\dfrac{b}{16}\)
Từ đó , ta được : \(b=16\cdot sin50^0\approx12,257\left(cm\right)\)
Vậy độ dài cạnh AC là xấp xỉ \(12,257cm\).

Vẽ đường kính AD của đường tròn (O). Ta thấy ngay \(\overrightarrow{OA}=\overrightarrow{DO}\), do đó \(\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\) \(=\overrightarrow{DO}+\overrightarrow{OB}+\overrightarrow{OC}\) \(=\overrightarrow{DB}+\overrightarrow{OC}\)
Mặt khác, \(\overrightarrow{OH}=\overrightarrow{OC}+\overrightarrow{CH}\) nên \(\overrightarrow{DB}=\overrightarrow{CH}\), từ đó suy ra tứ giác BDCH là hình bình hành \(\Rightarrow\left\{{}\begin{matrix}DB//CH\\DC//BH\end{matrix}\right.\). (*)
Trong đường tròn (O), có đường kính AD nên \(\widehat{ABD}=\widehat{ACD}=90^o\) hay \(\left\{{}\begin{matrix}DB\perp AB\\DC\perp AC\end{matrix}\right.\) (**)
Từ (*) và (**), suy ra \(\left\{{}\begin{matrix}CH\perp AB\\BH\perp AC\end{matrix}\right.\). Điều này đồng nghĩa với việc H là trực tâm tam giác ABC. (đpcm)