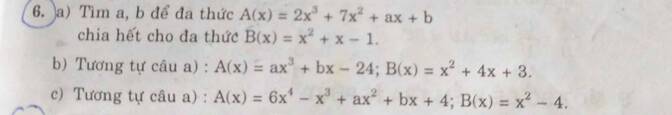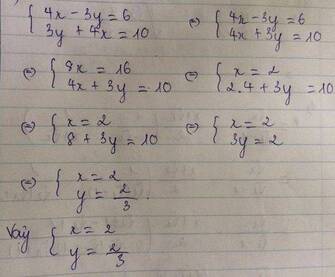
a)Vì |4x - 2| = 6 <=> 4x - 2 ϵ {6,-6} <=> x ϵ {2,-1}

Thay x = 2, ta có B không tồn tại

Thay x = -1, ta có B = \(\dfrac{1}{3}\)

b)ĐKXĐ:x ≠ 2,-2

Ta có \(A=\dfrac{5}{x+2}+\dfrac{3}{2-x}-\dfrac{15-x}{4-x^2}=\dfrac{10-5x+3x+6}{\left(x+2\right)\left(2-x\right)}-\dfrac{15-x}{4-x^2}=\dfrac{16-2x}{\left(x+2\right)\left(2-x\right)}-\dfrac{15-x}{4-x^2}=\dfrac{2x-16}{\left(x+2\right)\left(x-2\right)}-\dfrac{15-x}{4-x^2}=\dfrac{2x-16}{x^2-4}+\dfrac{15-x}{x^2-4}=\dfrac{x-1}{x^2-4}\)c)Từ câu b, ta có \(A=\dfrac{x-1}{x^2-4}\)\(\Rightarrow\dfrac{2A}{B}=\dfrac{\dfrac{\dfrac{2x-2}{x^2-4}}{2x+1}}{x^2-4}=\dfrac{2x-2}{2x+1}< 1\) với mọi x

Do đó không tồn tại x thỏa mãn đề bài

tui mới lớp 4

a, ta có A(x)=2x³+7x²+ax+b

                   =(2x³+2x²+2x)+(5x²+5x+5)+ax-7x+b-5

                   =2x(x²+x+1)+5(x²+x+1)+(a-7)x+(b-5)

                   =(x²+x+1)(2x+5)+(a-7)x+(b-5)

ta có: (x²+x+1)(2x+5)⋮B(x)

→để A(x)⋮B(x) thì (a-7)x+(b-5)=0

→\(\left\{{}\begin{matrix}a-7=0\\b-5=0\end{matrix}\right.\) ⇔\(\left\{{}\begin{matrix}a=7\\b=5\end{matrix}\right.\)

vậy ....

mk trình bày hơi tắt xíu 

bn cố gắng dịch nhé

\(B=x+1+\dfrac{25}{x+2}=x+2+\dfrac{25}{x+2}-1\)

Áp dụng bđt cauchy, ta có \(x+2+\dfrac{25}{x+2}\ge2.\sqrt{\left(x+2\right).\dfrac{25}{x+2}}=2.5=10\)

Do đó B ≥ 10 - 1 = 9

Dấu = xảy ra <=> x = 3

Nếu không có điều kiện gì bổ sung thêm thì biểu thức này không có max bạn nhé.

 Ta có:   m > n

=> 9m > 9n (nhân hai vế với 9)

=>  9m +1 > 9n +1 (cộng hai vế với 1)

Gọi chiều dài, chiều rộng của mảnh vườn lần lượt là a và b ( 0< a,b< 210; m)

Theo đề bài ta có hệ pt: 

2a + 2b = 110

4a + 8b = 316 

⇒ a = 31 (m)

    b = 24 (m) 

- Độ dài ban đầu:

+ Nửa chu vi HCN là: \(\dfrac{110}{2}=55\left(m\right)\)

+ Gọi chiều dài HCN là: \(a\left(m\right)\left(đk:0< a< 55\right)\)

+ Chiều rộng HCN là: \(55-a\left(m\right)\)

- Độ dài sau khi thay đổi:

+ Nửa chu vi HCN là: \(\dfrac{316}{2}=158\left(m\right)\)

+ Chiều dài HCN là: \(2a\left(m\right)\)

+ Chiều rộng HCN là: \(4\left(55-a\right)\left(m\right)\)

Theo bài ra, ta có phương trình:

\(2a+4\left(55-a\right)=158\\ \Leftrightarrow2a+220-4a=158\\ \Leftrightarrow2a-4a=158-220\\ \Leftrightarrow-2a=-62\\ \Leftrightarrow a=31\left(m\right)\left(TM\right)\)

Vậy chiều dài là 31m, chiều rộng là 55 - 31 = 22m