Ta thấy \(ab\le\dfrac{a^2+b^2}{2}=1\) và \(a+b\le\sqrt{2\left(a^2+b^2\right)}=2\). Áp dụng BĐT B.C.S, ta được \(P=\dfrac{a^4}{ba^2+a^2}+\dfrac{b^4}{ab^2+b^2}\) \(\ge\dfrac{\left(a^2+b^2\right)^2}{ba^2+ab^2+a^2+b^2}=\dfrac{2^2}{ab\left(a+b\right)+2}\ge\dfrac{4}{1.2+2}=1\)

ĐTXR \(\Leftrightarrow a=b=1\)

Vậy GTNN của P là 1 khi \(a=b=1\)

Ta có \(a+b^2\le\dfrac{a^2+1}{2}+b^2=\dfrac{a^2+2b^2+1}{2}\)

\(\Rightarrow\dfrac{2a^2}{a+b^2}\ge\dfrac{4a^2}{a^2+2b^2+1}=\dfrac{4a^4}{a^4+2b^2a^2+a^2}\). Lập 2 BĐT tương tự rồi áp dụng bất đẳng thức BCS, ta có:

\(\dfrac{2a^2}{a+b^2}+\dfrac{2b^2}{b+c^2}+\dfrac{2c^2}{c+a^2}\ge\dfrac{\left(2a^2+2b^2+2c^2\right)^2}{a^4+b^4+c^4+2\left(a^2b^2+b^2c^2+c^2a^2\right)+a^2+b^2+c^2}\) \(=\dfrac{4\left(a^2+b^2+c^2\right)^2}{\left(a^2+b^2+c^2\right)^2+3}\)\(=\dfrac{4.3^2}{3^2+3}=3\).

Mà \(a+b+c\le\sqrt{3\left(a^2+b^2+c^2\right)}=3\) nên ta có đpcm. ĐTXR \(\Leftrightarrow a=b=c=1\)

Anh gửi riêng phần phân tích này

\(x^6-2x^5y+2xy^5+y^6=\left(x^2+y^2\right)\left(x^4-x^2y^2+y^4\right)-2xy\left(x^2+y^2\right)\left(x^2-y^2\right)=\left(x^2+y^2\right).\left(x^4-x^2y^2+y^4-2xy\left(x^2-y^2\right)\right)=\left(x^2+y^2\right)\left(\left(x^4-2x^2y^2+y^4\right)-2xy\left(x^2-y^2\right)+x^2y^2\right)\)Viết tiếp cái ngoặc to thành bình phương là ra cái anh vt chỗ trên đầu nhé

Thử xem có đc ko

Vẫn đề đó hả em

Câu này dùng BĐT Schur là ra luôn cx đc, nhưng mà thế thì hơi mất hứng, anh thử đề xuất phương án này ha

VT=\(cyc\sum x^5.\left(x-y+z\right)\) Gấp đôi vế trái lên và phá ngoặc ra nhóm  về kiểu này

2.VT=(x^6-2x^5y+2xy^5+y^6)+.......tương tự như thế ha

       Giờ chỉ cần mỗi cái ngoặc này >=0 là cả lũ >=0 do tương tự

Mà \(x^6-2x^5y+2xy^5+y^6=\left(x^2+y^2\right).\left(x^2-xy-y^2\right)^2\)  (Cái này em nhóm 2 cái cuối, 2 cái giữa xong triển khai ra là đc)

       Dễ thấy x^2+y^2>=0, cái ngoặc kia là bình phương cũng >=0

 Do đó cái TH kia >=0. Các th còn lại thì cx tương tự

 Cộng vế với vế suy ra 2VT>=0, Hay VT>=0 (đpcm)

Gọi cạnh góc vuông bé là \(x\)  ( cm) ; \(x\) > 0

Thì cạnh góc vuông lớn là \(x\times\) 3 = 3\(x\)

Diện tích của tam giác vuông khi đó là: 3\(x\) \(\times\) \(x\) = 3\(x^2\)

Theo bài ra ta có: 3\(x^2\) = 150 ⇒ \(x^2\) = 150 : 3 ⇒ \(x^2\) = 50 

Theo py ta go ta có:

Độ dài cạnh huyền là: \(\sqrt{x^2+\left(3x\right)^2}\) = \(\sqrt{10x^2}\) = \(\sqrt{10.50}\) = 10\(\sqrt{5}\)

Kết luận độ dài cạnh huyền là: 10\(\sqrt{5}\)(cm)

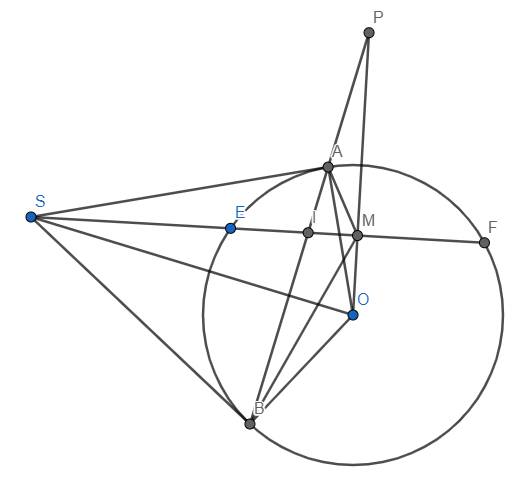
a) Do SA là tiếp tuyến tại A của (O) nên \(\widehat{OAS}=90^o\). Tương tự, ta có \(\widehat{OBS}=90^o\), suy ra \(\widehat{OAS}+\widehat{OBS}=180^o\). Do đó tứ giác SAOB nội tiếp. (đpcm)

 Mặt khác, trong đường tròn (O) có M là trung điểm của dây EF nên \(OM\perp EF\) tại M hay \(\widehat{OMS}=90^o\). Từ đó suy ra \(\widehat{OMS}=\widehat{OAS}\),từ đó tứ giác OMAS nội tiếp. Vì vậy 5 điểm O, M, A, S, B cùng thuộc một đường tròn \(\Rightarrow\) Tứ giác SAMO nội tiếp (đpcm)

b) Ta thấy tứ giác OMAB nội tiếp nên \(\widehat{PMA}=\widehat{PBO}\). Từ đó dễ dàng suy ra \(\Delta PAM~\Delta POB\left(g.g\right)\Rightarrow\dfrac{PA}{PO}=\dfrac{PM}{PB}\) \(\Rightarrow PA.PB=PO.PM\) (đpcm)

c) Do tứ giác SAMB nội tiếp nên \(\widehat{SMB}=\widehat{SAB}\) và \(\widehat{SMA}=\widehat{SBA}\). Mặt khác, trong đường tròn (O), có 2 tiếp tuyến tại A và B cắt nhau tại S nên \(SA=SB\) hay \(\Delta SAB\) cân tại S \(\Rightarrow\widehat{SAB}=\widehat{SBA}\) \(\Rightarrow\widehat{SMB}=\widehat{SMA}\) hay MI là phân giác trong của \(\widehat{AMB}\) . Lại có \(MP\perp MI\) nên MP là phân giác ngoài của \(\widehat{AMB}\). Áp dụng tính chất đường phân giác, ta thu được \(\dfrac{IA}{IB}=\dfrac{MA}{MB}\) và \(\dfrac{PA}{PB}=\dfrac{MA}{MB}\). Từ đây suy ra \(\dfrac{IA}{IB}=\dfrac{PA}{PB}\) \(\Rightarrow PA.IB=PB.IA\) (đpcm)

Đề thi chuyên SP hả em, bài này sử dụng Liên hợp với đánh giá em nhé:

Đầu tiên trừ 2 về mình có là
\(x\sqrt{y+4}+x\sqrt{y+11}-y\sqrt{x+4}-y\sqrt{x+11}=0\)

Từ hệ mình dễ dàng suy ra đc x,y>0

Anh liên hợp cho 1 cái nha

\(x\sqrt{y+4}-y\sqrt{x+4}=\sqrt{x^2y+4x^2}-\sqrt{y^2x+4y^2}=\dfrac{x^2y-y^2x+4x^2-4y^2}{\sqrt{.........}+\sqrt{.......}}=\left(x-y\right).\dfrac{xy+4x+4y}{\sqrt{.........}+\sqrt{............}}\)

Cái kia em cx liên hợp tương tự, đặt x-y của cả 2 cái khi liên hợp xong phương trình sẽ là

\(\left(x-y\right)\left(\dfrac{xy+4x+4y}{\sqrt{...}+\sqrt{...}}+\dfrac{xy+11x+11y}{\sqrt{........}+\sqrt{.....}}\right)=0\)  Cái trong ngoặc to đùng hiển nhiên >0 với x,y>0. DO đó x-y=0 hay x=y

 EM thế vào phương trình ban đầu thì có \(x\sqrt{x+4}+x\sqrt{x+11}=35\)

Đến đây thì nhẩm đc x=5 thoả mãn em giải bằng đánh giá:

 Với  x=5 suy ra......=35

Với x>5 suy ra......>35

Với x<5 suy ra.....<35

Kết luận đc x=5, do đó y=5

Note: hướng làm em nhé, bổ sung thêm điều kiện xác định linh tinh zô

Xem qua xem hiểu đc đến đâu em nhé