Cả mảnh vải dài :

  \(3,75\times100:75=5\left(m\right)\)

Nếu cắt đi 3/5 mảnh vải tức còn lại 2/5 mảnh vải . Vậy mảnh vải còn lại dài :

 \(5\times2:5=2\left(m\right)\)

Hiệu số tuổi của mẹ và con không bao giờ thay đổi đổi

Hiệu số phần bằng nhau là :

5 - 1 = 4 phần

Số tuổi của con sau 5 năm là :

28 : 4 x 1 = 7 tuổi

Số tuổi của con hiện nay là :

7 - 3 = 4 tuổi

Số tuổi của mẹ hiện nay là :

4 + 28 = 32 tuổi

Vì mỗi năm mỗi người sẽ thêm 1 tuổi nên hiệu số tuổi hai mẹ con luôn không đổi theo thời gian. Vây sau 3 năm nữa mẹ vẫn hơn con 28 tuổi.

Ta có sơ đồ: 

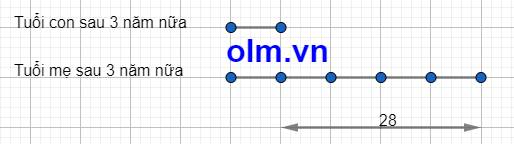
Tuổi con sau 3 năm nữa: 28 : (5-1) = 7 (tuổi)

Tuổi con hiện nay là: 7 - 3  = 4 (tuổi)

Tuổi mẹ hiện nay là: 4 + 28 = 32 (tuổi)

Đáp số: tuổi con hiện nay 4 tuổi; tuổi mẹ hiện nay 32 tuổi 

Tổng của chiều dài và chiều rộng là:

          960 : 2 = 480 (m)

Tổng số phần bằng nhau là:

          2 + 1 = 3 ( phần )

Chiều rộng trên bản đồ là:

          (480 : 3) x 1 = 160 (m)

Chiều dài trên bản đồ là:

          (480 : 3) x 2 = 320 (m)

Diện tích của mảnh đất là:

          320 x 160= 51200 (m2)

Diện tích của mảnh đất trên bản đồ tỉ lệ 1:1000 là:

          51200 : 1000 = 52,1 (m2)

Bài 5 :
Hiện nay mẹ hơn con 28 tuổi . Sau 3 năm nữa , tuổi mẹ gấp 5 lần tuổi con . Tính số tuổi của mỗi người hiện nay 

= 45 x 10 x 0,45 + 1,5 x 30 x 3 + 45 x 2,5 

= 45 x ( 4,5 + 2,5 ) + 1,5 x 30 x 3 

= 4,5 x 10 x 7 + 4,5 x 30 

= 4,5 x ( 70 + 30 ) 

= 4,5 x 100 = 450

Sửa đề : \(\dfrac{a^2}{a^2+b}+\dfrac{b^2}{b^2+a}\le1\\ \) (*)

\(< =>\dfrac{a^2\left(b^2+a\right)+b^2\left(a^2+b\right)}{\left(a^2+b\right)\left(b^2+a\right)}\le1\\ < =>a^2b^2+a^3+b^2a^2+b^3\le\left(a^2+b\right)\left(b^2+a\right)\) ( Nhân cả 2 vế cho `(a^{2}+b)(b^{2}+a)>0` )

\(< =>a^3+b^3+2a^2b^2\le a^2b^2+b^3+a^3+ab\\ < =>a^2b^2\le ab\\ < =>ab\le1\) ( Chia 2 vế cho `ab>0` )

Do a,b >0 

Nên áp dụng BDT Cô Si :

\(2\ge a+b\ge2\sqrt{ab}< =>\sqrt{ab}\le1\\ < =>ab\le1\)

Do đó (*) luôn đúng

Vậy ta chứng minh đc bài toán

Dấu "=" xảy ra khi : \(a=b>0,a+b=2< =>a=b=1\)

Với x, y là hai số dương, dễ dàng chứng minh x + y  2,

do x + y = 2  => 0 < xy ≤ 1 (1)

Ta lại có: 2xy( x2 + y2) ≤ 

=> 0 < 2xy(x2 + y2)  ≤ (x+y)4/4 = 4

=> 0 < xy( x2 + y2) ≤ 2 (2)

Nhân (1) với (2) theo vế ta có: x2y2 ( x2 + y2) ≤ 2 (đpcm)

Dấu “=” xảy ra khi x = y = 1

4h tổ 1 làm được  :

    \(4:9=\dfrac{4}{9}\) (cv)

1h tổ 2 làm được :

   \(1:12=\dfrac{1}{12}\) (cv)

Tổ 2 còn phải làm :

   \(1-\dfrac{4}{9}=\dfrac{5}{9}\)(cv)

Vậy phần việc còn lại tổ 2 làm trong :

  \(\dfrac{5}{9}:\dfrac{1}{12}=\dfrac{20}{3}\left(h\right)\)